Kinh Nghiệm về Cách tìm phương trình tiếp tuyến nhanh Mới Nhất
Người Hùng đang tìm kiếm từ khóa Cách tìm phương trình tiếp tuyến nhanh 2022-04-01 12:26:06 san sẻ Kinh Nghiệm Hướng dẫn trong nội dung bài viết một cách 2022.
Bài giảng: Cách viết phương trình tiếp tuyến của đồ thị hàm số – Cô Nguyễn Phương Anh (Giáo viên VietJack) Quảng cáo 1. Ý nghĩa hình học của đạo hàm Cho hàm số y = f(x) có đồ thị (C) và điểm. M0 (x0; y0) ∈ (C) Tiếp tuyến của đồ thị (C) tại điểm M0 có dạng y = f'(x0 )(x – x0 ) + y0 Trong số đó: Điểm M0 (x0; y0) ∈(C) được gọi là tiếp điểm ( với y0 = f(x0)). k = f’x0) là thông số góc của tiếp tuyến. Chú ý: Đường thẳng bất kỳ trải qua M0 (x0; y0) có thông số góc k, có phương trình y = k(x – x0 ) + y0 Cho hai tuyến phố thẳng Δ1:y = k1 x + m1 và Δ2:y = k2 x + mét vuông Lúc đó: 2. Điều kiện tiếp xúc của hai đồ thị Cho hai hàm số y = f(x),(C) và y = g(x),(C’) (C) và (C’ ) tiếp xúc nhau khi chỉ khi hệ phương trình
Nghiệm của hệ là hoành độ tiếp điểm của hai đồ thị đó. Đặc biệt: Đường thẳng y = kx + m là tiếp tuyến với (C):y = f(x) khi chỉ khi hệ 3. Các dạng phương trình tiếp tuyến thường gặp Cho hàm số y = f(x) gọi đồ thị của hàm số là (C) Dạng 1. Viết phương trình tiếp tuyến của đồ thị hàm số (C):y = f(x) tại M0 (x0; y0) Phương pháp Bước 1. Tính y’ = f’ (x) suy ra thông số góc của phương trình tiếp tuyến là k = y’ (x0). Bước 2. Phương trình tiếp tuyến của đồ thị (C) tại điểm M0 (x0; y0) có dạng y – y0 = f'(x0)(x – x0) Dạng 2. Viết phương trình tiếp tuyến của đồ thị hàm số (C):y = f(x) có thông số góc k cho trước. Phương pháp Bước 1. Gọi M0 (x0; y0) là tiếp điểm và tính y’ = f’ (x). Bước 2. Hệ số góc tiếp tuyến là k = f’ (x0). . Giải phương trình này tìm kiếm được x0 thay vào hàm số được y0. Bước 3. Với mỗi tiếp điểm ta tìm kiếm được những tiếp tuyến tương ứng d: y – y0 = f’ (x0)(x – x0) Chú ý: Đề bài thường cho thông số góc tiếp tuyến dưới những dạng sau: Tiếp tuyến d Δ:y = ax + b ⇒ thông số góc của tiếp tuyến là k = a Tiếp tuyến d Δ:y = ax + b(a ≠ 0)⇒ thông số góc của tiếp tuyến là k = -1/a Tiếp tuyến tạo với trục hoành một góc α thì thông số góc của tiếp tuyến d là k = ±tanα Dạng 3. Viết phương trình tiếp tuyến của đồ thị hàm số (C):y = f(x) biết tiếp tuyến trải qua điểm A(xA; yA) Phương pháp Cách 1. Bước 1: Phương trình tiếp tuyến trải qua A(xA; yA) thông số góc k có dạng d:y = k(x – xA ) + yA (*) Bước 2: là tiếp tuyến của khi và chỉ khi hệ sau có nghiệm: Bước 3: Giải hệ này tìm kiếm được x suy ra k và thế vào phương trình (*), ta được tiếp tuyến cần tìm. Cách 2. Bước 1. Gọi M(x0; f(x0 )) là tiếp điểm và tính thông số góc tiếp tuyến k = y'(x0 ) = f’ (x0) theo x0 Bước 2. Phương trình tiếp tuyến có dạng d = y'(x0 )(x – x0 ) + y0 (**). Do điểm A(xA; yA) ∈ d nên yA = y'(x0 )(xA – x0 ) + y0 giải phương trình này ta tìm kiếm được x0 . Bước 3. Thế x0 vào (**) ta được tiếp tuyến cần tìm. Quảng cáo Ví dụ 1: Cho hàm số (C):y = x3 + 3×2. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M(1; 4). Hướng dẫn Ta có y’ = 3×2 + 6x; y'(1) = 9 Phương trình tiếp tuyến của đồ thị hàm số tại điểm M(1; 4) là: y = 9(x – 1) + 4 = 9x – 5 Ví dụ 2: Cho hàm số (C):y = 4×3 – 6×2 + 1. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến trải qua điểm A(-1; -9). Hướng dẫn Ta có y’ = 12×2 – 12x Gọi M(x0, y0) là tọa độ tiếp điểm Phương trình tiếp tuyến của (C) tại điểm M có dạng: y = (12×02 – 12×0> )(x – x0 ) + 4×03 – 6×02 + 1 Vì tiếp tuyến trải qua điểm A(-1; -9) nên ta có: -9 = (12×02 – 12×0 )( -1 – x0 ) + 4×03 – 6×03 + 1 Với Khi đó phương trình tiếp tuyến cần tìm là y = 15/4 (x – 5/4) – 9/16 = 15/4 x – 21/4 Với x0 = -1 thì Khi đó phương trình tiếp tuyến cần tìm là y = 24(x + 1) – 9 = 24x + 15 Ví dụ 3: Cho hàm số (C): Hướng dẫn ĐKXĐ: x ≠ -2. Ta có y’ = 3/(x + 2)2 . Phương trình Δ:3x – y + 2 = 0 hay Δ:y = 3x + 2 Gọi tọa độ tiếp điểm là M(x0, y0) Vì tiếp tuyến tuy nhiên tuy nhiên với đường thẳng có phương trình Δ:3x – y + 2 = 0 nên ta có Với x0 = -1 Khi đó phương trình tiếp tuyến cần tìm là y = 3(x + 1) – 1 = 3x + 2 (loại). Với x0 = -3 Khi đó phương trình tiếp tuyến cần tìm là y = 3(x + 3) + 5 = 3x + 14 (thỏa mãn thị hiếu) Quảng cáo Câu 1: Cho hàm số y = -2×3 + 6×2 – 5. Viết phương trình tiếp tuyến của (C) tại điểm M có hoành độ bằng 3. Ta có y’ = -6×2 + 12x; y’ (3) = -18; y(3) = -5 Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 3 là y = -18(x – 3) – 5 = -18x + 49 Câu 2: Cho hàm số (C):y = 1/4×4 – 2×2. Viết phương trình tiếp tuyến của (C) tại điểm M có hoành độ x0 > 0 biết rằng y” (x0 )= -1. Ta có y’ = x3 – 4x; y” = 3×2 – 4 Vì y” (x0 ) = -1 ⇒ 3×02 – 4 = -1 ⇒ x02 = 1 ⇒ x0 = 1 (Vì x0 > 0) Với x0 = 1 ⇒ y0 = -7/4 ; y0′ = -3. Khi đó phương trình tiếp tuyến tại điểm M là: y = -3(x – 1) – 7/4 = -3x + 5/4 Câu 3: Gọi d là tiếp tuyến của đồ thị hàm số (C):y =(x – 5)/(-x + 1) tại điểm A của (C) và trục hoành. Viết phương trình của d. Hoành độ giao điểm của (C) và trục hoành là nghiệm của phương trình (x – 5)/(-x + 1) = 0 ⇒ x = 5 Khi đó tọa độ điểm A = (5; 0) ĐKXĐ x ≠ 1. Ta có y’= (-4)/(-x + 1)2 ; y'(5) = -1/4 Phương trình đường thẳng d đó là phương trình tiếp tuyến tại điểm A(5;0) có dạng y = -1/4 (x – 5) = -1/4 x + 5 /4 Câu 4: Cho đồ thị hàm số y = 3x – 4×2 có đồ thị (C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến trải qua điểm A(1; 3). Ta có y’ = 3 – 8x Gọi M(x0 , y0) là tọa độ tiếp điểm Phương trình tiếp tuyến của (C) tại điểm M có dạng: y = (3 – 8×0 )(x – x0 ) + 3×0 – 4×02 Vì tiếp tuyến trải qua điểm A(1; 3) nên ta có: 3 = (3 – 8×0 )(1 – x0 ) + 3×0 – 4×02 Với x0 = 0 thì Khi đó phương trình tiếp tuyến cần tìm là y = 3(x – 0) + 0 = 3x Với x0 = 2 thì Khi đó phương trình tiếp tuyến cần tìm là y = -13(x – 2) – 10 = -13x + 16 Câu 5: Cho hàm số y = x3 – 3×2 + 6x + 1 có đồ thị (C). Viết phương trình tiếp tuyến có thông số góc nhỏ nhất. Gọi M(x0,y0) là tọa độ tiếp điểm. Ta có y’ = 3×2 – 6x + 6 Khi đó y’ (x0 )=3×02 – 6×0 + 6 = 3(x02 – 2×0 + 2) = 3[(x0 – 1)2 + 1] ≥ 3 Vậy thông số góc nhỏ nhất của tiếp tuyến là y’ (x0) = 3, dấu bằng xẩy ra khi x0 = 1 Với x0 = 1 thì Khi đó phương trình tiếp tuyến cần tìm là y = 3(x – 1) + 5 = 3x + 2 Câu 6: Cho hàm số (C):y = x3 – 3x + 2. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đó có thông số góc bằng 9. Gọi M(x0, y0) là tọa độ tiếp điểm. Ta có y’ = 3×2 – 3 Khi đó y'(x0 ) = 3×02 – 3 = 9 Với x0 = 2 thì Khi đó phương trình tiếp tuyến cần tìm là y = 9(x – 2) + 4 = 9x – 14 Với x0 = -2 thì Khi đó phương trình tiếp tuyến cần tìm là y = 9(x + 2) + 0 = 9x + 18 Câu 7: Cho hàm số y = (-x + 5)/(x + 2) có đồ thị là (C). Viết phương trình tiếp tuyến của (C) sao cho tiếp tuyến đó tuy nhiên tuy nhiên với đường thẳng d:y = -1/7 x + 5/7 ĐKXĐ: x ≠ -2. Ta có y’ = (-7)/(x + 2)2 . Gọi tọa độ tiếp điểm là M(x0, y0) Vì tiếp tuyến tuy nhiên tuy nhiên với đường thẳng có phương trình d:y = -1/7 x + 5/7 nên ta có Với Khi đó phương trình tiếp tuyến cần tìm là y = -1/7 (x – 5) + 0 = -1/7 x + 5/7 (loại). Với x0 = -9 Khi đó phương trình tiếp tuyến cần tìm là y = -1/7 (x + 9) – 2 = -1/7 x – 23/7 (thỏa mãn thị hiếu). Câu 8: Viết phương trình tiếp tuyến của đồ thị hàm số y = -x4 – 2×2 + 3 vuông góc với đường thẳng Δ: x – 8y + 2017 = 0 Ta có y’= -4×3 – 4x. Gọi tọa độ tiếp điểm là M(x0, y0) Phương trình Δ:x – 8y + 2017 = 0 hay Δ: y = 1/8 x + 2017/8 Vì tiếp tuyến vuông góc với đường thẳng có phương trình d:y = 1/8 x + 2017/8 nên ta có y'(x0 ) = -8 hay -4×03 – 4×0 = -8 ⇔ x0 = 1 Với Khi đó phương trình tiếp tuyến cần tìm là y = -8(x – 1) + 0 = -8x + 8 (thỏa mãn thị hiếu). Câu 9: Viết phương trình tiếp tuyến của đồ thị hàm số y = 1/3 x3 + 1/2 x2 – 2x + 1 và tiếp tuyến tạo với đường thẳng d:x + 3y – 1 = 0 một góc 450. Gọi tọa độ tiếp điểm là M(x0, y0). Có y’ = x2 + x – 2 Phương trình đường thẳng d: x + 3y – 1 = 0 ⇔ y = -1/3 x + 1/3 Vì tiếp tuyến tạo với đường thẳng d: x + 3y – 1 = 0 một góc 450 nên ta có Với
Với x0 = 0 ⇒ y(x0 )= 1. Phương trình tiếp tuyến cần tìm là: y = -2(x – 0) + 1 = -2x + 1 x0 = -1 ⇒ y(x0 ) = 19/6. Phương trình tiếp tuyến cần tìm là: y = -2(x + 1) + 19/6 = -2x + 7/6 Vậy những phương trình tiếp tuyến cần tìm là: y = -2x + 1; y = -2x + 7/6 Xem thêm những dạng bài tập Toán lớp 12 có trong đề thi THPT Quốc gia khác: Giới thiệu kênh Youtube VietJack tiep-tuyen.jsp Video tương quan |
Chia sẻ
đoạn Clip Cách tìm phương trình tiếp tuyến nhanh ?
Một số hướng dẫn một cách rõ ràng hơn về Video Cách tìm phương trình tiếp tuyến nhanh tiên tiến và phát triển nhất .
ShareLink Download Cách tìm phương trình tiếp tuyến nhanh miễn phí
Heros đang tìm một số trong những Chia Sẻ Link Cập nhật Cách tìm phương trình tiếp tuyến nhanh Free.
#Cách #tìm #phương #trình #tiếp #tuyến #nhanh



 có nghiệm.
có nghiệm. có nghiệm.
có nghiệm.

 .
.  .
.  . Viết phương trình tiếp tuyến của (C) biết tiếp tuyến tuy nhiên tuy nhiên với đường thẳng có phương trình Δ:3x – y + 2 = 0
. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến tuy nhiên tuy nhiên với đường thẳng có phương trình Δ:3x – y + 2 = 0



 .
.  .
. 

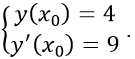
 .
. 





 . Phương trình tiếp tuyến cần tìm là:
. Phương trình tiếp tuyến cần tìm là:
 . Phương trình tiếp tuyến cần tìm là:
. Phương trình tiếp tuyến cần tìm là:

 ;
;

