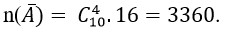Kinh Nghiệm Hướng dẫn Có 8 quyển sách Địa Lý 12 quyển sách Lịch sử 2022
Bann đang tìm kiếm từ khóa Có 8 quyển sách Địa Lý 12 quyển sách Lịch sử 2022-04-10 16:38:03 san sẻ Bí kíp về trong nội dung bài viết một cách 2021.
Quảng cáo Ví dụ 1: Một người bỏ ngẫu nhiên bốn lá thư vào 4 bì thư đã được ghi địa chỉ. Tính xác suất của biến cố A: “ Có tối thiểu một lá thư bỏ đúng phong bì của nó”. A.5/8 B.3/8 C.1/8 D. 0.24 Hướng dẫn giải : Đáp án : A Số cách bỏ 4 lá thư vào 4 bì thư là: Kí hiệu 4 lá thư là: L1;L2;L3;L4 và bộ (L1;L2;L3;L4) là một hóan vị của những số 1;2;3;4 trong số đó Li =i ; i =1,4 nếu lá thư Li bỏ đúng địa chỉ. Ta xét những kĩ năng sau : + Có 4 lá thư bỏ đúng địa chỉ:(1;2;3;4) nên có một cách bỏ + Có 2 là thư bỏ đúng địa chỉ: + Số cách bỏ 2 lá thư đúng địa chỉ là: + khi đó có một cách bỏ hai là thư còn sót lại Nên trường hợp này còn có: Có đúng 1 lá thư bỏ đúng địa chỉ: Số cách chọn lá thư bỏ đúng địa chỉ: 4 cách Số cách chọn bỏ ba lá thư còn sót lại: 2.1=2 cách Nên trường hợp này còn có: 4.2=8 cách bỏ. Do đó: n(A)= 1+ 6+ 8= 15 Vậy P(A)= 15/24= 5/8. Ví dụ 2: Một thầy giáo có 10 cuốn sách rất khác nhau trong số đó có 4 cuốn sách Toán, 3 cuốn sách Vậy Lí và 3 cuốn sách Hóa Học. Thầy giáo muốn lấy ra 5 cuốn và tặng cho 5 học viên A: B: C; D; E mỗi em một cuốn. Hỏi thầy giáo có bao nhiêu cách tặng nếu sau khoản thời hạn tặng sách xong, mỗi một trong ba loại sách trên đều còn sót lại tối thiểu một cuốn. A.5/13 B.4/21 C.17/21 D.409/666 Hướng dẫn giải : Đáp án : C + Không gian mẫu là số cách chọn ngẫu nhiên 5 trong 10 cuốn sách rồi tặng cho 5 học viên. Suy ra số thành phần của không khí mẫu là + Gọi A là biến cố Sau khi tặng sách thì mỗi một trong ba loại sách của thầy giáo còn sót lại tối thiểu một cuốn . Để tìm số thành phần của A, ta tìm số thành phần của biến cố A , tức sau khoản thời hạn tặng sách có môn không hề lại cuốn nào. Vì tổng số sách của hai loại bất kỳ to nhiều hơn 5 cuốn nên không thể chọn sao cho cùng hết 2 loại sách. Do vậy chỉ trọn vẹn có thể một môn hết sách, ta có những kĩ năng: Cách tặng sao cho không hề sách Toán, tức là ta tặng 4 cuốn sách toán, 1 cuốn còn sót lại Lý hoặc Hóa + 4 cuốn sách Toán tặng cho 4 người trong 5 người, có + 1 người còn sót lại được tặng 1 cuốn trong 6 cuốn (Lý và Hóa), có Suy ra có Tương tự, có Tương tự, có Suy ra số thành phần của biến cố A là|ΩA |=720+2520+2520=5760. Suy ra số thành phần của biến cố A là|ΩA|=|Ω|-|ΩA |=30240-5760=24480. Vậy xác suất cần tính Quảng cáo Ví dụ 3: Một hộp chứa 5 viên bi đỏ, 6 viên bi xanh và 7 viên bi trắng. Chọn ngẫu nhiên 6 viên bi từ hộp, tính xác suất để được 6 viên bi có cả ba màu đồng thời hiệu của số bi xanh và bi đỏ, hiệu của số bi trắng và số bi xanh, hiệu của số bi đỏ và số bi trắng theo thứ tự là ba số hạng liên tục của một cấp số cộng. A.5/13 B.4/21 C.17/21 D.40/221 Hướng dẫn giải : Đáp án : D Không gian mẫu là số cách chọn ngẫu nhiên 6 viên bi từ hộp chứa 18 viên bi. Suy ra số thành phần của không khí mẫu là Gọi A là biến cố 6 viên bi được chọn có cả ba màu đồng thời hiệu của số bi xanh và bi đỏ, hiệu của số bi trắng và số bi xanh, hiệu của số bi đỏ và số bi trắng theo thứ tự là ba số hạng liên tục của một cấp số cộng . Gọi x ;y ;z lần lượt là số bi đỏ, bi xanh và bi trắng được lấy. Suy ra + Hiệu của số bi xanh và bi đỏ là y-x. + Hiệu của số bi trắng và bi xanh là z-y. + Hiệu của số bi đỏ và bi trắng là x-z. Theo giả thiết, ta có (y-x) – (x-z)=2(z-y) Hay y=z. Do đó biến cố A được phát biểu lại như sau 6 viên bi được chọn có cả ba màu đồng thời số bi xanh bằng số bi trắng . Ta có những trường hợp thuận tiện cho biến cố A như sau: Trường hợp 1. Chọn 2 viên bi đỏ, 2 viên bi xanh và 2 viên bi trắng. Do đó trường hợp này còn có Trường hợp 2. Chọn 4 viên bi đỏ, 1 viên bi xanh và 1 viên bi trắng. Do đó trường hợp này còn có Suy ra số thành phần của biến cố A là Vậy xác suất cần tính : Ví dụ 4: Một hộp chứa 12 viên bi kích thước như nhau, trong số đó có 5 viên bi màu xanh được đánh số từ là một trong những đến 5; có 4 viên bi red color được đánh số từ là một trong những đến 4 và 3 viên bi màu vàng được đánh số từ là một trong những đến 3. Lấy ngẫu nhiên 2 viên bi từ hộp, tính xác suất để 2 viên bi được lấy vừa khác màu vừa khác số. A.8/33 B.14/33 C.29/66 D.37/66 Hướng dẫn giải : Đáp án : D Không gian mẫu là số sách lấy tùy ý 2 viên từ hộp chứa 12 viên bi. Suy ra số thành phần của không khí mẫu là Gọi A là biến cố 2 viên bi được lấy vừa khác màu vừa khác số . + Số cách lấy 2 viên bi gồm: 1 bi xanh và 1 bi đỏ là 4.4= 16 cách (do số bi đỏ thấp hơn nên ta lấy trước, có 4 cách lấy bi đỏ. Tiếp tục lấy bi xanh nhưng không lấy viên trùng với số của bi đỏ nên có 4 cách lấy bi xanh). + Số cách lấy 2 viên bi gồm: 1 bi xanh và 1 bi vàng là 3.4= 12 cách. + Số cách lấy 2 viên bi gồm: 1 bi đỏ và 1 bi vàng là 3.3= 9 cách. Suy ra số thành phần của biến cố A là |ΩA | = 16+ 12+ 9= 37. Vậy xác suất cần tính P(A)= 37/66 Ví dụ 5: Cho tập hợp A= 0,1,2,3,4,5. Gọi S là tập hợp những số có 3 chữ số rất khác nhau được lập thành từ những chữ số của tập A. Chọn ngẫu nhiên một số trong những từ S, tính xác suất để số được chọn có chữ số cuối gấp hai chữ số đầu. A.1/5 B.23/25 C.2/25 D.4/5 Quảng cáo Hướng dẫn giải : Đáp án : C + Gọi số cần tìm của tập S có dạng abc Trong số đó: Khi đó + Số cách chọn chữ số a có 5 cách chọn vì a≠0 . + Số cách chọn chữ số b có 5 cách chọn vì b≠a. + Số cách chọn chữ số c có 4 cách chọn vì c≠a;c≠b. Do đó tập S có 5.5.4= 100 thành phần. Không gian mẫu là chọn ngẫu nhiên 1 số ít từ tập S. Suy ra số thành phần của không khí mẫu là + Gọi X là biến cố “Số được chọn có chữ số cuối gấp hai chữ số đầu”. Khi đó ta có những bộ số là 1b2 hoặc 2b4 thỏa mãn thị hiếu biến cố X và cứ mỗi bộ thì b có 4 cách chọn nên có toàn bộ 4+ 4= 8 số thỏa yêu cầu. Suy ra số thành phần của biến cố X là n(X)= 8. Vậy xác suất cần tính:P(X)= 8/100=2/25 Ví dụ 6: Cho tập hợp A=2,3,4,5,6,7,8. Gọi S là tập hợp những số tự nhiên có 4 chữ số đôi một rất khác nhau được lập thành từ những chữ số của tập A. Chọn ngẫu nhiên một số trong những từ S, tính xác suất để số được chọn mà trong những số luôn luôn xuất hiện hai chữ số chẵn và hai chữ số lẻ. A.1/5 B.3/35 C.17/35 D.18/35 Hướng dẫn giải : Đáp án : D Số thành phần của tập S là Không gian mẫu là chọn ngẫu nhiên 1 số ít từ tập S. Suy ra số thành phần của không khí mẫu là Gọi X là biến cố “ Số được chọn luôn luôn xuất hiện hai chữ số chẵn và hai chữ số lẻ “. Số cách chọn hai chữ số chẵn từ bốn chữ số 2,4,6,8 là Số cách chọn hai chữ số lẻ từ ba chữ số 3,5,7 là Từ bốn chữ số được chọn ta lập số có bốn chữ số rất khác nhau, số cách lập tương ứng với một hoán vị của 4 thành phần nên có 4! cách. Suy ra số thành phần của biến cố X là n(X)= 6.3. 4!= 432 . Vậy xác suất cần tính P(X)= 432/840= 18/35. Ví dụ 7: Gọi S là tập hợp những số tự nhiên có 3 chữ số đôi một rất khác nhau được lập thành từ những chữ số 1,2,3,4,6. Chọn ngẫu nhiên một số trong những từ S, tính xác xuất để số được chọn chia hết cho 3 A.1/10 B.3/5 C.2/5 D.1/15 Hướng dẫn giải : Đáp án : C – Số thành phần của S là Không gian mẫu là chọn ngẫu nhiên 1 số ít từ tập S. Suy ra số thành phần của không khí mẫu là – Gọi A là biến cố “ Số được chọn chia hết cho 3”. Từ 5 chữ số đã cho ta có bộ gồm ba chữ số có tổng chia hết cho 3 là(1,2,3); (1,2,6); ( 2,3,4) và (2,4,6). Mỗi bộ ba chữ số này ta lập được 3!= 6 số thuộc tập hợp S. Suy ra số thành phần của biến cố A là n(A)= 6.4= 24 . Vậy xác suất cần tính P(A)= 24/60= 2/5 Ví dụ 8: Đội tuyển học viên giỏi của một trường THPT có 8 học viên nam và 4 học viên nữ. Trong buổi lễ trao phần thưởng, những học viên trên được xếp thành một hàng ngang. Tính xác suất để khi xếp sao cho 2 học viên nữ không đứng cạnh nhau. A.14/55 B.25/660 C.23/55 D.19/660 Hướng dẫn giải : Đáp án : A – Không gian mẫu là số cách sắp xếp toàn bộ 12 học viên thành một hàng ngang. Suy ra số thành phần của không khí mẫu là n(Ω)= 12! . – Gọi A là biến cố “ Xếp những học viên trên thành một hàng ngang mà 2 học viên nữ không đứng cạnh nhau”. Ta mô tả kĩ năng thuận tiện của biến cố A như sau: Đầu tiên xếp 8 học viên nam thành một hàng ngang, có 8! cách. Sau đó xem 8 học viên này như 8 vách ngăn nên có 9 vị trí để xếp 4 học viên nữ thỏa yêu cầu bài toán (gồm 7 vị trí giữa 8 học viên và 2 vị trí hai đầu). Do đó có Suy ra số thành phần của biến cố A là Vậy xác suất cần tính : Ví dụ 9: Có 3 bì thư giống nhau lần lượt được đánh số thứ tự từ là một trong những đến 3 và 3 con tem giống nhau lần lượt đánh số thứ tự từ là một trong những đến 3. Dán 3 con tem đó vào 3 bì thư sao cho không tồn tại bì thư nào không tồn tại tem. Tính xác suất để lấy ra được 2 bì thư trong 3 bì thư trên sao cho từng bì thư đều phải có số thứ tự giống với số thứ tự con tem đã dán vào nó. A.5/6 B.1/6 C.2/3 D.1/2 Hướng dẫn giải : Đáp án : B – Không gian mẫu là số cách dán 3 con tem trên 3 bì thư, tức là hoán vị của 3 con tem trên 3 bì thư. Suy ra số thành phần của không khí mẫu là n(Ω)= 3!= 6 – Gọi A là biến cố “ 2 bì thư lấy ra có số thứ tự giống với số thứ tự con tem đã dán vào nó” Thế thì bì thư còn sót lại cũng luôn có thể có số thứ tự giống với số thứ tự con tem đã dán vào nó. Trường hợp này còn có một cách duy nhất Suy ra số thành phần của biến cố A là n(A)= 1 Vậy xác suất cần tính là P(A)= 1/6 Ví dụ 10: Trong thư viện có 12 quyển sách gồm 3 quyển Toán giống nhau, 3 quyển Lý giống nhau, 3 quyển Hóa giống nhau và 3 quyển Sinh giống nhau. Tính xác suất để xếp thành một dãy sao cho 3 quyển sách thuộc cùng 1 môn không được xếp liền nhau? A.1/28512 B.1/299376 C.1/14256 D.1/7128 Hướng dẫn giải : Đáp án : A – Không gian mẫu là xếp 12 quyển sách thành một dãy nên số thành phần của không khí mẫu là: n(Ω)= 12! – Gọi A là biến cố xếp 12 quyển thành dãy sao cho 3 quyển sách thuộc cùng một môn không được xếp cạnh nhau. Ta tính số những kết quả thuận tiện cho biến cố A: Xếp 3 cuốn sách Toán kề nhau. Xem 3 cuốn sách Toán là 3 vách ngăn, giữa 3 cuốn sách Toán có 2 vị trí trống và thêm hai vị trí hai đầu, tổng số có 4 vị trí trống. + Bước 1. Chọn 3 vị trí trống trong 4 vị trí để xếp 3 cuốn Lý, có + Bước 2. Giữa 6 cuốn Lý và Toán có 5 vị trí trống và thêm 2 vị trí hai đầu, tổng số có 7 vị trí trống. Chọn 3 vị trí trong 7 vị trí trống để xếp 3 cuốn Hóa, có + Bước 3. Giữa 9 cuốn sách Toán, Lý và Hóa đã xếp có 8 vị trí trống và thêm 2 vị trí hai đầu, tổng số có 10 vị trí trống. Chọn 3 vị trí trong 10 vị trí trống để xếp 3 cuốn Sinh, có Vậy theo quy tắc nhân số kĩ năng thuận tiện cho A là: 4. 35. 120= 16800 cách ⇒ Xác suất biến cố A là: P(A)= 16800/12!= 1/28512 Ví dụ 11: Một lớp học có 30 học viên gồm có cả nam và nữ. Chọn ngẫu nhiên 3 học viên để tham gia hoạt động giải trí và sinh hoạt của Đoàn trường. Xác suất chọn được 2 nam và 1 nữ là 12/29. Tính số học viên nữ của lớp. A.16 B.14 C.13 D.17 Hướng dẫn giải : Đáp án : B – Gọi số học viên nữ của lớp là n( n∈N*;n≤28). Suy ra số học viên nam là 30- n. – Không gian mẫu là chọn bất kì 3 học viên từ 30 học viên. Vậy số học viên nữ của lớp là 14 học viên. Ví dụ 12 : Một chi đoàn có 3 đoàn viên nữ và một số trong những đoàn viên nam. Cần lập một đội nhóm thanh niên tình nguyện (TNTN) gồm 4 người. Biết xác suất để trong 4 người được chọn có 3 nữ bằng 2/5 lần xác suất 4 người được chọn toàn nam. Hỏi chi đoàn đó có bao nhiêu đoàn viên. A.9 B.10 C.11 D.12 Hướng dẫn giải : Đáp án : A + Gọi số đoàn viên trong chi đoàn đó là n(n≥7;n∈N*) Suy ra số đoàn viên nam trong chi đoàn là n- 3 Vậy đoàn có 9 đoàn viên. Ví dụ 13: Một hộp có 10 phiếu, trong số đó có 2 phiếu trúng thưởng. Có 10 người lần lượt lấy ngẫu nhiên từng người 1 phiếu. Tính xác suất người thứ ba lấy được phiếu trúng thưởng. A.4/5 B.3/5 C.1/5 D.2/5 Hướng dẫn giải : Đáp án : C Không gian mẫu là từng người lấy ngẫu nhiên 1 phiếu. Suy ra số thành phần của không khí mẫu là n(Ω)= 10! . Gọi A là biến cố “ Người thứ ba lấy được phiếu trúng thưởng”. Ta mô tả kĩ năng thuận tiện của biến cố A như sau: + Người thứ ba có + 9 người còn sót lại sở hữu số cách lấy phiếu là 9!. Suy ra số thành phần của biến cố A là n(A)= 2.9!. Vậy xác suất cần tính P(A)= 2.9!/10!= 1/5 Ví dụ 14: Trong kỳ thi THPT Quốc Gia, mỗi lớp thi gồm 24 thí sinh được sắp xếp vào 24 bàn rất khác nhau. Bạn Nam là một thí sinh tham dự cuộc thi, bạn Đk 4 môn thi và cả 4 lần thi đều thi tại một phòng duy nhất. Giả sử giám thị xếp thí sinh vào vị trí một cách ngẫu nhiên, tính xác xuất để trong 4 lần thi thì bạn Nam có đúng gấp đôi ngồi cùng vào một trong những vị trí. A.253/1152 B.899/1152 C.17/288 D.21/576 Hướng dẫn giải : Đáp án : A – Không gian mẫu là số cách ngẫu nhiên chỗ ngồi trong 4 lần thi của Nam. Suy ra số thành phần của không khí mẫu là n(Ω)= 244 . – Gọi A là biến cố “ 4 lần thi thì bạn Nam có đúng gấp đôi ngồi cùng vào một trong những vị trí”. Ta mô tả không khí của biến cố A như sau: + Trong 4 lần có gấp đôi trùng vị trí, có + Giả sử lần thứ nhất có 24 cách chọn chỗ ngồi, lần thứ hai trùng với lần thứ nhất có một cách chọn chỗ ngồi. Hai lần còn sót lại thứ ba và thứ tư không trùng với những lần trước và cũng không trùng nhau nên có 23.22 cách. Suy ra số thành phần của biến cố A là n(A)= Vậy xác suất cần tính : Câu 1: Cho tập hợp A= 1,2,3,4,5. Gọi S là tập hợp toàn bộ những số tự nhiên có tối thiểu 3 chữ số, những chữ số đôi một rất khác nhau được lập thành từ những chữ số thuộc tập A. Chọn ngẫu nhiên một số trong những từ S, tính xác xuất để số được chọn có tổng những chữ số bằng 10. A.1/30 B.3/25 C.7/25 D.7/30 Đáp án : B Ta tính số thành phần thuộc tập S như sau: Suy ra số thành phần của tập S là : Không gian mẫu là chọn ngẫu nhiên 1 số ít từ tập S. Suy ra số thành phần của không khí mẫu là : + Gọi X là biến cố “ Số được chọn có tổng những chữ số bằng 10”. Các tập con của A có tổng số thành phần bằng 10 là A1= 1,2,3,4; A2= 2,3,5; A3= 1,4,5. + Từ A1 lập được những số thuộc S là 4!. + Từ A2 lập được những số thuộc S là 3!. + Từ A3 lập được những số thuộc S là 3!. Suy ra số thành phần của biến cố X là n(X)= 4!+ 3!+ 3!= 36 Vậy xác suất cần tính : P(X)= 36/300= 3/25 Câu 2: Có 20 tấm thẻ được đánh số từ là một trong những đến 20. Chọn ngẫu nhiên ra 8 tấm thẻ, tính xác suất để sở hữu 3 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn trong số đó chỉ có đúng một tấm thẻ mang số chia hết cho 10. A.560/4199 B.4/15 C.11/15 D.3639/4199 Đáp án : A – Không gian mẫu là cách chọn 8 tấm thể trong 20 tấm thẻ. Suy ra số thành phần của không mẫu là – Gọi A là biến cố “ 3 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn trong số đó chỉ có đúng một tấm thẻ mang số chia hết cho 10”. Để tìm số thành phần của A ta làm như sau: + Đầu tiên chọn 3 tấm thẻ trong 10 tấm thẻ mang số lẻ, có + Tiếp theo chọn 4 tấm thẻ trong 8 tấm thẻ mang số chẵn (không chia hết cho 10 ), có + Sau cùng ta chọn một trong 2 tấm thẻ mang số chia hết cho 10, có Suy ra số thành phần của biến cố A là Vậy xác suất cần tính : Câu 3: Gọi S là tập hợp những số tự nhiên có hai chữ số. Chọn ngẫu nhiên đồng thời hai số từ tập hợp S. Tính xác suất để hai số được chọn có chữ số hàng cty chức năng giống nhau. A.8/89 B.17/89 C.17/178 D.31/178 Đáp án : A – Số thành phần của tập S là 9.10= 90. Không gian mẫu là chọn ngẫu nhiên 2 số từ tập S. Suy ra số thành phần của không khí mẫu là n(Ω)= – Gọi X là biến cố “ Số được chọn có chữ số hàng cty chức năng giống nhau”. Ta mô tả không khí của biến cố X như sau: + Chọn chữ số hàng cty chức năng của hai số giống nhau: có 10 cách chọn chữ số hàng cty chức năng (chọn từ những chữ số 0,1,2,…,9). + Chọn chữ số hàng trăm của hai số: có Suy ra số thành phần của biến cố X là n(X)= 10. Vậy xác suất cần tính P(X)= 360/4005= 8/89 Câu 4: Gọi S là tập hợp những số tự nhiên gồm 9 chữ số rất khác nhau. Chọn ngẫu nhiên một số trong những từ S, tính xác suất để chọn được một số trong những gồm 4 chữ số lẻ và chữ số 0 luôn đứng giữa hai chữ số lẻ (hai số hai bên chữ số 0 là số lẻ). A.49/54 B.5/54 C.17/54 D.11/54 Đáp án : B – Số thành phần của tập S là Không gian mẫu là chọn ngẫu nhiên 1 số ít từ tập S. Suy ra số thành phần của không khí mẫu là n(Ω)= – Gọi X là biến cố “ Số được chọn gồm 4 chữ số lẻ và chữ số 0 luôn đứng giữa hai chữ số lẻ”. Do số 0 luôn đứng giữa 2 số lẻ nên số 0 không đứng ở vị trí thứ nhất và vị trí ở đầu cuối. Ta có những kĩ năng + Chọn 1 trong những 7 vị trí để xếp số 0, có + Chọn 2 trong 5 số lẻ và xếp vào 2 vị trí cạnh số 0 vừa xếp, có + Chọn 2 số lẻ trong 3 số lẻ còn sót lại và chọn 4 số chẵn từ 2,4,6,8 tiếp sau đó xếp 6 số này vào 6 vị trí trống còn sót lại sở hữu Suy ra số thành phần của biến cố X là : Vậy xác suất cần tính : Câu 5: Một người bỏ ngẫu nhiên 4 lá thư và 4 chiếc phong bì thư đã để sẵn địa chỉ. Xác suất để sở hữu tối thiểu một lá thư bỏ đúng địa chỉ là. A.5/8 B.2/3 C.3/8 D.1/3 Đáp án : A + Gọi 4 lá thư lần lượt là A; B;C; D và 4 phong bì thư có địa chỉ đúng với những lá thư trên lần lượt là một trong những,2,3,4. Số thành phần không khí mẫu là n(Ω)= 4!= 24. + Gọi X là biến cố “ có tối thiểu một lá thư bỏ đúng địa chỉ”. Ta có những trường hợp sau: Tường Hợp 1: Cả 4 lá thư đều bỏ đúng địa chỉ: Chỉ có một trường hợp duy nhất Tường Hợp 2: Có đúng 2 lá thư bỏ đúng địa chỉ. Có 6 trường hợp xẩy ra là: A1- B2- C4- D3; A1- B4- C3- D2; A4- B2- C3- D1; A1- B3- C2- D4; A3- B2- C1- D4 hoặc A2- B1- C3- D4 Tường Hợp 3: Có đúng 1 lá thư bỏ đúng địa chỉ: Chỉ có lá thư A bỏ đúng địa chỉ thì có 2 trường hợp A1- B3- C4- D2; A1- B4- C2- D3 Tương tự với lá thư B có 2 trường hợp. Lá thư C chỉ có đúng 2 trường hợp. Lá thư D chỉ có đúng 2 trường hợp. Suy ra có 8 trường hợp chỉ có đúng 1 lá thư bỏ đúng địa chỉ. Vậy số thành phần của biến cố X là n(X)= 1+ 6+ 8 = 15 Nên xác suất cần tính là: P(X)= 15/24= 5/8. Câu 6: Giải bóng chuyền VTV Cup gồm 9 đội bóng tham gia, trong số đó có 6 đội quốc tế và 3 đội của Việt Nam. Ban tổ chức triển khai cho bốc thăm ngẫu nhiên để phân thành 3 bảng A; B; C và mỗi bảng có 3 đội. Tính xác suất để 3 đội bóng của Việt Nam ở 3 bảng rất khác nhau. A.3/56 B.19/28 C.9/28 D.53/56 Đáp án : C Câu 7: Trong giải cầu lông kỷ niệm ngày truyền thống cuội nguồn học viên sinh viên có 8 người tham gia trong số đó có hai bạn Việt và Hoàng. Các vận động viên được chia thành hai bảng A và B, mỗi bảng gồm 4 người. Giả sử việc chia bảng tiến hành bằng phương pháp bốc thăm ngẫu nhiên, tính xác suất để cả hai bạn Việt và Hoàng nằm chung 1 bảng đấu. A.6/7 B.3/7 C.3/4 D.2/5 Đáp án : B Câu 8: Một bộ đề thi toán học viên giỏi lớp 12 mà mỗi đề gồm 5 câu được chọn từ 15 câu dễ, 10 câu trung bình và 5 câu khó. Một đề thi được gọi là “Tốt” nếu trong đề thi có cả ba câu dễ, trung bình và khó, đồng thời số câu dễ quá nhiều hơn thế nữa 2. Lấy ngẫu nhiên một đề thi trong bộ đề trên. Tìm xác suất để đề thi lấy ra là một đề thi “ Tốt”. A.985/1566 B.235/783 C.3/7 D.625/1566 Đáp án : D Số thành phần của không khí mẫu là : Gọi A là biến cố “Đề thi lấy ra là một đề thi Tốt”. Vì trong một đề thi tốt có cả ba câu dễ, trung bình và khó, đồng thời số câu dễ quá nhiều hơn thế nữa 2 nên ta có những trường hợp tại đây thuận tiện cho biến cố A. Suy ra số thành phần của biến cố A là Vậy xác suất cần tính : Câu 9: Xếp 6 học viên nam và 4 học viên nữ vào một trong những bàn tròn 10 ghế. Tính xác suất để không tồn tại hai học viên nữ ngồi cạnh nhau. A.37/42 B.5/42 C.7/504 D.1/6 Đáp án : B – Không gian mẫu là xếp 6 học viên nam và 4 học viên nữ vào một trong những bàn tròn 10 ghế. ⇒ Số thành phần của không khí mẫu là: n(Ω)= 9! – Gọi A là biến cố “ không tồn tại hai học viên nữ ngồi cạnh nhau”. Ta mô tả kĩ năng thuận tiện của biến cố A như sau: + Đầu tiên ta cố định và thắt chặt 1 học viên nam, 5 học viên nam còn sót lại sở hữu 5! cách xếp. + Ta xem 6 học viên nam như 6 vách ngăn trên vòng tròn, thế thì sẽ tạo ra 6 ô trống để ta xếp 4 học viên nữ vào (mỗi ô trống chỉ được xếp 1 học viên nữ). Do đó có Suy ra số thành phần của biến cố A là n(A)= 5!. Vậy xác suất cần tính: P(A)= (5!. Câu 10: Có 4 hành quý khách bước lên một đoàn tàu gồm 4 toa. Mỗi hành quý khách độc lập với nhau và chọn ngẫu nhiên một toa. Tính xác suất để 1 toa có 3 người, 1 toa có một người, 2 toa còn sót lại không tồn tại ai. A.3/4 B.3/16 C.13/16 D.1/4 Đáp án : B – Không gian mẫu là số cách sắp xếp 4 hành quý khách lên 4 toa tàu. Vì mỗi hành quý khách có 4 cách chọn toa nên có 44 cách xếp. Suy ra số thành phần của không khí mẫu là n(Ω)= 44 . – Gọi A là biến cố “ 1 toa có 3 người, 1 toa có một người, 2 toa còn sót lại không tồn tại ai”. Để tìm số thành phần của A, ta chia thành hai quá trình như sau: + Giai đoạn thứ nhất. Chọn 3 hành quý khách trong 4 hành quý khách, chọn một toa trong 4 toa và xếp lên toa đó 3 hành quý khách vừa chọn. Suy ra có + Giai đoạn thứ hai. Chọn 1 toa trong 3 toa còn sót lại và xếp lên toa đó 1 một hành quý khách còn sót lại. Suy ra có Suy ra số thành phần của biến cố A là n(A)= 16.3= 48. Vậy xác suất cần tính P(A)= 48/44 = 3/16. Câu 11: Có 8 người quý khách bước ngẫu nhiên vào một trong những shop có 3 quầy.Tính xác suất để sở hữu 3 người cùng đến quầy thứ nhất? A.106/729 B.203/2187 C.2375/6561 D.1792/6561 Đáp án : D + Không gian mẫu là số cách sắp xếp 8 người quý khách vào 3 quầy. Vì từng người quý khách có 3 cách chọn quầy nên có 38 kĩ năng xẩy ra. Suy ra số thành phần của không khí mẫu là n(Ω)= 38. + Gọi A là biến cố “ Có 3 người cùng đến quầy thứ nhất, 5 người còn sót lại đến quầy thứ hai hoặc ba”. Để tìm số thành phần của A, ta chia thành hai quá trình như sau: Giai đoạn thứ nhất. Chọn 3 người quý khách trong 8 người quý khách và cho tới quầy thứ nhất, có Giai đoạn thứ hai. Còn lại 5 người quý khách xếp vào 2 quầy. Mỗi người quý khách có 2 cách chọn quầy. Suy ra có 25 cách xếp. Suy ra số thành phần của biến cố A là : Vậy xác suất cần tính : Câu 12: Một lớp học có 40 học viên trong số đó có 4 cặp bạn hữu sinh đôi. Trong cuộc họp thời gian đầu xuân mới thầy giáo chủ nhiệm lớp muốn lựa chọn ra 3 học viên để làm cán sự lớp. Tính xác suất để lựa chọn ra 3 học viên làm cán sự lớp mà không tồn tại cặp bạn hữu sinh đôi nào. A.64/65 B.12/65 C.98/130 D.Đáp án khác Đáp án : A + Không gian mẫu là số cách chọn ngẫu nhiên 3 học viên trong 40 học viên. Suy ra số thành phần không khí mẫu là : + Gọi A là biến cố “ 3 học viên được chọn không tồn tại cặp bạn hữu sinh đôi nào”. Để tìm số thành phần của A ta đi tìm số thành phần của biến cố đối A: 3 học viên được chọn luôn có một cặp bạn hữu sinh đôi. Suy ra số thành phần của biến cố A là n(A)= 4.38= 152. Suy ra số thành phần của biến cố A là n(A)= 9880 – 152 = 9728. Vậy xác suất cần tính P(A)= 9728/9880=64/65 Câu 13: Một người dân có 10 đôi giày rất khác nhau và trong lúc đi du lịch vội vã lấy ngẫu nhiên 4 chiếc. Tính xác suất để trong 4 chiếc giày lấy ra có tối thiểu một đôi. A.3/7 B.13/64 C.99/323 D.224/323 Đáp án : C – Không gian mẫu là số cách chọn ngẫu nhiên 4 chiếc giày từ 20 chiếc giày. Suy ra số thành phần của không khí mẫu là : – Gọi A là biến cố “ 4 chiếc giày lấy ra có tối thiểu một đôi”. + Để tìm số thành phần của biến cố A, ta đi tìm số thành phần của biến cố đối A là 4 chiếc giày được chọn không tồn tại đôi nào. + Số cách chọn 4 đôi giày từ 10 đôi giày là + Mỗi đôi lựa chọn ra 1 chiếc, thế thì mỗi chiếc có Suy ra số thành phần của biến cố Alà Suy ra số thành phần của biến cố A là n(A)= 4845 – 3360 = 1485. Vậy xác suất cần tính P(A)= 1485/4845 = 99/323. Xem thêm những dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác: Giới thiệu kênh Youtube VietJack
Đã có app VietJack trên điện thoại cảm ứng, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi trực tuyến, Bài giảng….miễn phí. Tải ngay ứng dụng trên Android và iOS. Nhóm học tập facebook miễn phí cho teen 2k5: fb.com/groups/hoctap2k5/ Theo dõi chúng tôi miễn phí trên social facebook và youtube: Nếu thấy hay, hãy động viên và san sẻ nhé! Các phản hồi không phù thích phù hợp với nội quy phản hồi website sẽ bị cấm phản hồi vĩnh viễn. to-hop-xac-suat.jsp Video tương quan |
Chia sẻ
đoạn Clip Có 8 quyển sách Địa Lý 12 quyển sách Lịch sử ?
Một số hướng dẫn một cách rõ ràng hơn về đoạn Clip Có 8 quyển sách Địa Lý 12 quyển sách Lịch sử tiên tiến và phát triển nhất .
Chia SẻLink Tải Có 8 quyển sách Địa Lý 12 quyển sách Lịch sử miễn phí
Bạn đang tìm một số trong những Share Link Down Có 8 quyển sách Địa Lý 12 quyển sách Lịch sử miễn phí.
#Có #quyển #sách #Địa #Lý #quyển #sách #Lịch #sử


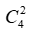
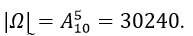
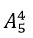 cách.
cách.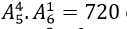 .
.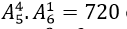 cách tặng sao cho không hề sách Toán.
cách tặng sao cho không hề sách Toán.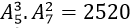 cách tặng sao cho không hề sách Lý.
cách tặng sao cho không hề sách Lý.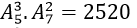 cách tặng sao cho không hề sách Hóa.
cách tặng sao cho không hề sách Hóa.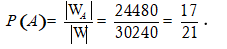 .
.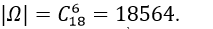
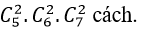
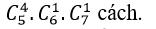
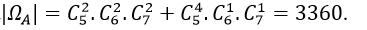
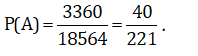
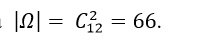
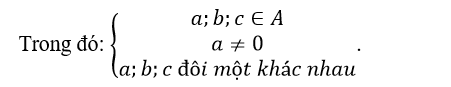
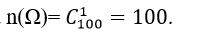
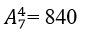
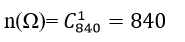
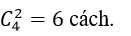
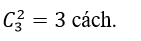
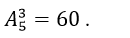
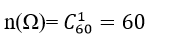
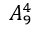 cách xếp 4 học viên nữ.
cách xếp 4 học viên nữ.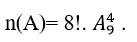
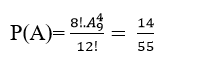
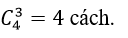
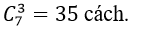
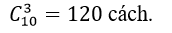
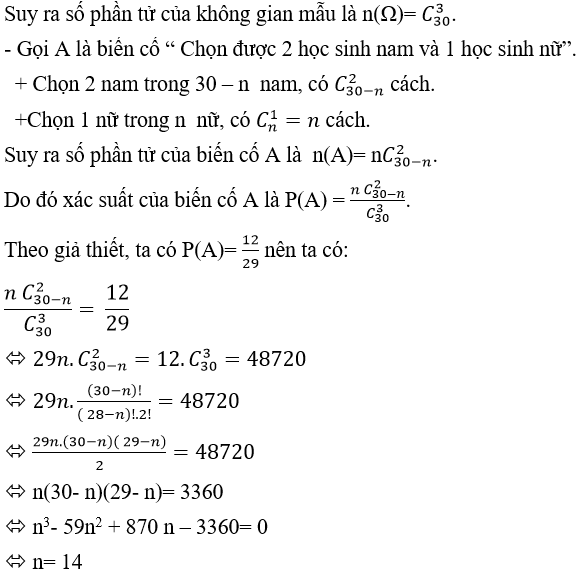
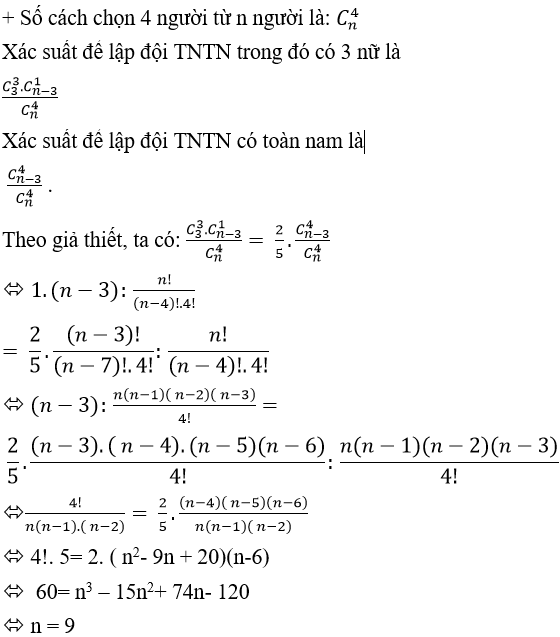
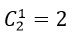 kĩ năng lấy được phiếu trúng thưởng.
kĩ năng lấy được phiếu trúng thưởng.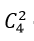 cách.
cách.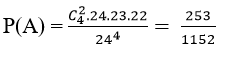

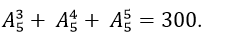
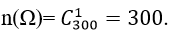
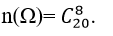 .
.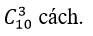
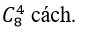
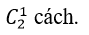
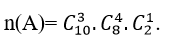
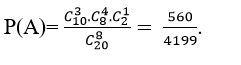
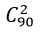 =4005.
=4005.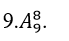
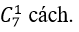
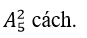
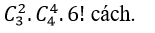
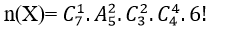
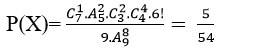


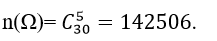

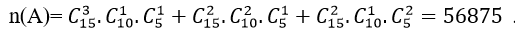
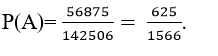
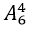 cách xếp.
cách xếp.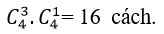
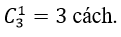
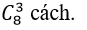
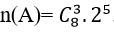

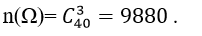
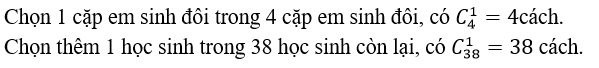
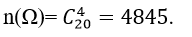
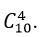
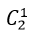 cách chọn. Suy ra 4 chiếc có
cách chọn. Suy ra 4 chiếc có