Đồ thị hàm số bậc 2 là gì 2021

Bí kíp về Đồ thị hàm số bậc 2 là gì Mới Nhất

Pro đang tìm kiếm từ khóa Đồ thị hàm số bậc 2 là gì 2022-04-05 10:56:04 san sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách 2021.

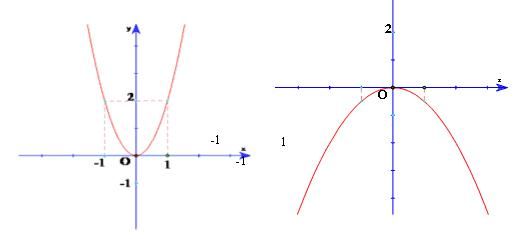
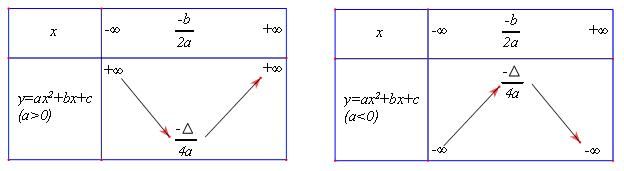
1. Các kiến thức và kỹ năng cần nhớ Sự đồng biến và nghịch biến của hàm số $y = ax^2,,left( a ne 0 right)$ +) Nếu (a > 0) thì hàm số nghịch biến khi (x < 0) và đồng biến khi (x > 0). +) Nếu (a < 0) thì hàm số đồng biến khi (x < 0) và nghịch biến khi (x > 0). Đồ thị hàm số $y = ax^2,,left( a ne 0 right)$ Đồ thị của hàm số $y = ax^2,,left( a ne 0 right)$ là một đường cong trải qua gốc tọa độ $O$ và nhận trục $Oy$ làm trục đối xứng. Đường cong đó là một parabol với đỉnh $O$. – Nếu (a > 0) thì đồ thị nằm phía trên trục hoành, $O$ là yếu tố thấp nhất của đồ thị. – Nếu (a < 0) thì đồ thị nằm phía dưới trục hoành, $O$ là vấn tôn vinh nhất của đồ thị. 2. Các dạng toán thường gặp Dạng 1: Tính giá trị của hàm số tại một điểm cho trước Phương pháp: Giá trị của hàm số (y = ax^2left( a ne 0 right)) tại điểm (x = x_0) là $y_0 = ax_0^2$. Dạng 2: Bài toán tương quan đến tính đồng biến và nghịch biến của hàm số Phương pháp: Xét hàm số (y = ax^2left( a ne 0 right).) Ta có: – Nếu (a > 0) thì hàm số nghịch biến khi (x < 0) và đồng biến khi (x > 0). – Nếu (a < 0) thì hàm số đồng biến khi (x < 0) và nghịch biến khi (x > 0). Dạng 3: Các bài toán tương quan đến đồ thị hàm số (y = ax^2left( a ne 0 right)) Phương pháp: Để vẽ đồ thị hàm số (y = ax^2left( a ne 0 right)) ta tiến hành tiến trình sau Bước 1: Lập bảng giá trị đặc biệt quan trọng tương ứng giữa $x$ và $y$ của hàm số $y = ax^2,,(a ne 0)$. Bước 2: Biểu diễn những điểm đặc biệt quan trọng trên mặt phẳng tọa độ và vẽ đồ thị dạng parabol của hàm số trải qua những điểm đặc biệt quan trọng đó. Dạng 4: Tọa độ giao điểm của parabol và đường thẳng Phương pháp: Cho parabol $(P):y=ax^2(a ne 0)$ và đường thẳng $d:y = mx + n$. Để tìm tọa độ giao điểm (nếu có) của $(d)$ và $(P)$, ta làm như sau: Bước 1. Xét phương trình hoành độ giao điểm của $(d)$ và $(P)$: $ax^2 = mx + n$ (*) Bước 2. Giải phương trình (*) ta tìm kiếm được nghiệm (nếu có). Từ đó ta tìm kiếm được tọa độ giao điểm của $(d)$ và $(P)$ . HÀM SỐ BẬC HAI Quan tâm 0 Đưa vào sổ tay 1. Định nghĩa Hàm số bậc hai là hàm số được cho bằng biểu thức có dạng $y = ax^2 + bx + c$, trong số đó a, b, c là những hằng số với $a ne 0$ 2. Đồ thị của hàm số bậc hai a, Nhắc lại về đồ thị hàm số $y = textatextx^2,,(a ne 0)$ Ta đã biết, đồ thị hàm số $y = textatextx^2,,(a ne 0)$là parabol $left( P_0 right)$ có những điểm lưu ý sau: 1.Đỉnh của parabol $left( P_0 right)$ là gốc tọa độ O 2.Parabol $left( P_0 right)$ có trục đối xứng là trục tung; 3.Parabol $left( P_0 right)$ hướng bề lõm lên trên khi a>0 và xuống dưới khi a<0 Chẳng hạn hình 2.16 là parabol $y = 2textx^2$; hình 2.17 là parabol y=$ – frac12x^2$ Hình 2.16 Hình 2.17 b, Đồ thị hàm số $y = ax^2 + bx + c$ Đồ thị của hàm số $y = textatextx^2 + bx + c,(a ne 0)$là một parabol có đỉnh $Ileft( – fracb2a; – fracDelta 4a right)$, nhận đường thẳng $x = – fracb2a$ làm trục đối xứng và hướng bề lõm lên trên khi a>0, xuống dưới khi a<0. CÁCH VẼ PARABOL – Xác định đỉnh của parabol; – Xác định trục đối xứng và hướng bề lõm của parabol; – Xác định một số trong những điểm cụ thế của parabol (ví dụ nổi bật nổi bật, giao điểm của parabol với những trục tọa độ và những điểm đối xứng với chúng qua trục đối xứng) 3. Sự biến thiên của hàm số bậc hai Từ đồ thị của hàm số bậc hai, ta suy ra bảng biến thiên tại đây: Bảng biến thiên : Như vậy Khi $a>0$, hàm số nghịch biến trên khoảng chừng $left( – infty ; – fracb2a right)$, đồng biến trên khoảng chừng$left( – fracb2a; + infty right)$và có mức giá trị nhỏ nhất là $ – fracDelta 4a$khi $x = – fracb2a$. Khi $a<0$, hàm số đồng biến trên khoảng chừng $left( – infty ; – fracb2a right)$, nghịch biến trên khoảng chừng$left( – fracb2a; + infty right)$và có mức giá trị lớn số 1 là $ – fracDelta 4a$khi $x = – fracb2a$. Hàm số bậc hai hủy Trợ giúp Nhập tối thiểu 8 ký tự, tối đa 255 ký tự. Thẻ Hàm số bậc hai ×29 Số người xem 7027 HÌNH HỌC 10 Vectơ Tích vô vị trí hướng của hai vectơ và ứng dụng Phương pháp toạ độ trong mặt phẳng ĐẠI SỐ 10 Mệnh đề, tập hợp Hàm số số 1 và bậc hai Phương trình và hệ phương trình Bất đẳng thức và bất phương trình Thống kê Góc lượng giác và công thức lượng giác ĐẠI SỐ VÀ GIẢI TÍCH 11 Hàm số lượng giác và phương trình lượng giác Tổ hợp và xác xuất Dãy số. Cấp số cộng và cấp số nhân Giới hạn Đạo hàm HÌNH HỌC 11 Phép dời hình và phép đồng dạng trong mặt phẳng Đường thẳng và mặt phẳng trong không khí. Quan hệ tuy nhiên tuy nhiên. Vectơ trong không khí. Quan hệ vuông góc. GIẢI TÍCH 12 Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Hàm số luỹ thừa, hàm số mũ, hàm số lôgarit Nguyên hàm, tích phân và ứng dụng Số phức HÌNH HỌC 12 Khối đa diện và thể tích của chúng Mặt cầu, mặt trụ, mặt nón Phương pháp toạ độ trong không khí CÔNG THỨC Công thức lượng giác Hệ thức lượng trong tam giác Công thức đạo hàm Tổ hợp – xác suất Liên quan Bài 104518 Bài 104470 Bài 104257 Bài 104026 Bài 102264 Video tương quan

Chia sẻ

Review Đồ thị hàm số bậc 2 là gì ?

Một số hướng dẫn một cách rõ ràng hơn về đoạn Clip Đồ thị hàm số bậc 2 là gì tiên tiến và phát triển nhất .

ShareLink Download Đồ thị hàm số bậc 2 là gì miễn phí

Bạn đang tìm một số trong những Chia Sẻ Link Down Đồ thị hàm số bậc 2 là gì Free.

#Đồ #thị #hàm #số #bậc #là #gì