Kinh Nghiệm về Phương trình cosx = a có nghiệm khi và chỉ khi Mới Nhất
Quý quý khách đang tìm kiếm từ khóa Phương trình cosx = a có nghiệm khi và chỉ khi 2022-04-10 19:02:03 san sẻ Bí kíp Hướng dẫn trong nội dung bài viết một cách Mới Nhất.
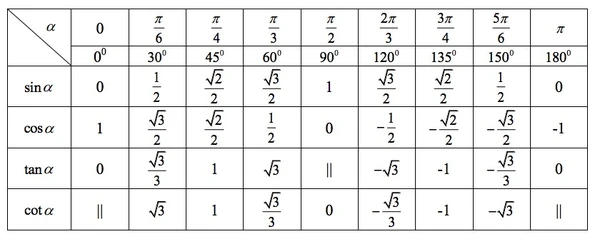
Phương trình lượng giác cosx = m
Điều kiện có nghiệm -1 ≤ m ≤ 1 m là giá trị sin của góc lượng giác đặc biệt quan trọng
m không phải là giá trị sin của góc đặc biệt quan trọng: cosx = m → x = ± arc cos(m) + k2π Ví dụ 1: Giải những phương trình lượng giác Hướng dẫn giải toán Bài tập vận dụng Bài tập 1 Bài tập 2 trong: Toán học, Toán học lớp 11, Đại số Xem mã nguồn
x = α + k2.π hoặc x = pi – α + k2.π (α: rad, k∈Z) x = a + k.360° hoặc x = 180° – a + k.360° (a: độ°, k∈Z)
x = ±α + k2.pi (α: rad, k∈Z) x = ±a + k.360° (a: độ°, k∈Z)
<=> x = α + k.pi (α: rad, k∈Z) <=> x = a + k.360° (α: độ°, k∈Z)
cotx=m
<=> x = α + k.pi (α: rad, k∈Z) <=> x = a + k.360° (α: độ°, k∈Z)
Một số dạng toánBiến đổi
Tìm nghiệm và số nghiệm1) Giải phương trình A với x ∈ a.
2) Tìm số nghiệm k
Tìm giâ trị lớn số 1 và nhỏ nhất
Tìm nghiệm âm lớn số 1 và nghiệm dương nhỏ nhất1) Với nghiệm âm lớn số 1
2) Với nghiệm dương nhỏ nhất
Tìm tập giá trịTìm tập giá trị của phương trình A.
Điều kiện Video tương quan |
Chia sẻ
Review Phương trình cosx = a có nghiệm khi và chỉ khi ?
Một số hướng dẫn một cách rõ ràng hơn về Video Phương trình cosx = a có nghiệm khi và chỉ khi tiên tiến và phát triển nhất .
Chia Sẻ Link Down Phương trình cosx = a có nghiệm khi và chỉ khi miễn phí
Người Hùng đang tìm một số trong những Chia Sẻ Link Cập nhật Phương trình cosx = a có nghiệm khi và chỉ khi Free.
#Phương #trình #cosx #có #nghiệm #khi #và #chỉ #khi

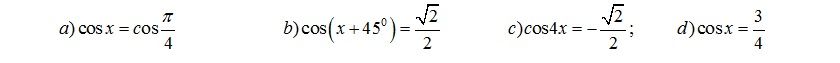
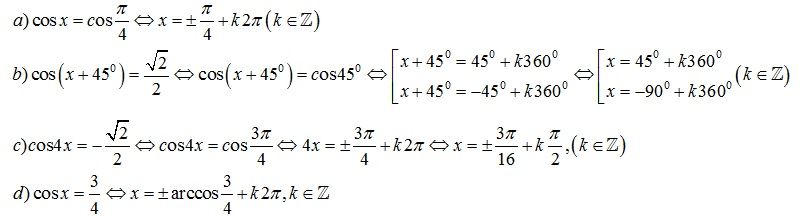
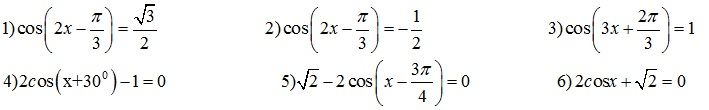
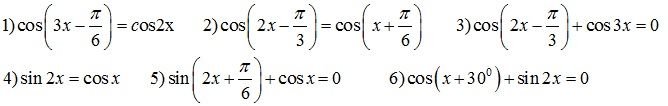
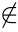 [-1;1] => phương trình vô nghiệm
[-1;1] => phương trình vô nghiệm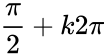
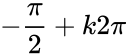

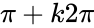

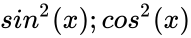 , ta thường “hạ bậc tăng cung”.
, ta thường “hạ bậc tăng cung”.

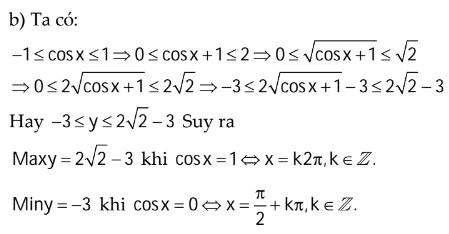
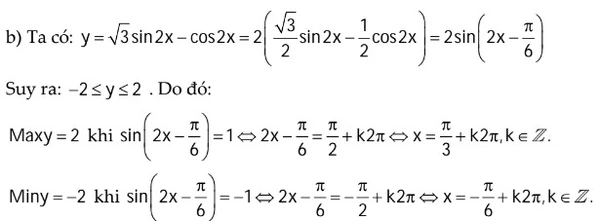


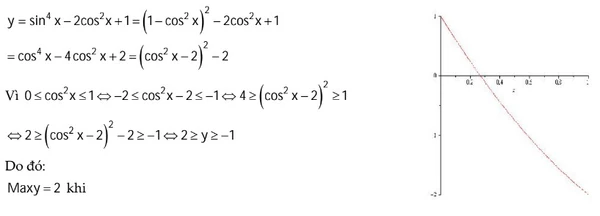

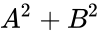 ≥
≥ 