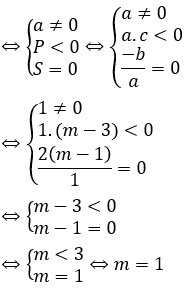Thủ Thuật về Tập hợp những giá trị của m để phương trình x^2+mx-m+1=0 có hai nghiệm trái dấu 2021
Pro đang tìm kiếm từ khóa Tập hợp những giá trị của m để phương trình x^2+mx-m+1=0 có hai nghiệm trái dấu 2022-04-07 09:26:05 san sẻ Bí kíp về trong nội dung bài viết một cách Mới Nhất.
Với Tìm m để phương trình bậc hai có hai nghiệm cùng dấu, trái dấu Toán lớp 9 gồm khá đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải rõ ràng sẽ tương hỗ học viên ôn tập, biết phương pháp làm dạng bài tập Tìm m để phương trình bậc hai có hai nghiệm cùng dấu, trái dấu từ đó đạt điểm trên cao trong bài thi môn Toán lớp 9. – Cho phương trình ax2 + bx + c = 0 (a ≠ 0). Khi đó + Điều kiện để phương trình có 2 nghiệm trái dấu: a.c < 0 + Điều kiện để phương trình có 2 nghiệm cùng dấu: ( nếu là 2 nghiệm phân biệt cùng dấu ta thay ∆ ≥ 0 bởi ∆ > 0) + Điều kiện để phương trình có 2 nghiệm cùng dấu dương: ( nếu là 2 nghiệm phân biệt cùng dấu ta thay ∆ ≥ 0 bởi ∆ > 0) + Điều kiện để phương trình có 2 nghiệm cùng dấu âm: ( nếu là 2 nghiệm phân biệt cùng dấu ta thay ∆ ≥ 0 bởi ∆ > 0) Ví dụ 1: Tìm m để phương trình x2 – (mét vuông + 1)x + mét vuông – 7m + 12 = 0 có hai nghiệm trái dấu Giải Phương trình có 2 nghiệm trái dấu khi a.c < 0 Vậy với 3 < m < 4 thì phương trình có hai nghiệm trái dấu Ví dụ 2: Tìm m để phương trình 3×2 – 4mx + m < 2 – 2m – 3 = 0 có hai nghiệm phân biệt cùng dấu Giải Phương trình có 2 nghiệm phân biệt cùng dấu khi Vậy với m > 3 hoặc m < -1 thì phương trình có hai nghiệm phân biệt cùng dấu Ví dụ 3: Tìm m để phương trình x2 – (2m + 3)x + m = 0 có hai nghiệm phân biệt cùng dấu âm < /p.> Giải Phương trình có 2 nghiệm phân biệt cùng dấu âm khi Không có mức giá trị nào của m thỏa mãn thị hiếu (1), (2) và (3) Vậy không tồn tại m thỏa mãn thị hiếu đề bài Câu 1: Cho phương trình x2 – 2x – 1 = 0 (m là tham số). Tìm xác lập đúng A. Phương trình luôn có hai nghiệm trái dấu. B. Phương trình vô nghiệm < /p.> C. Phương trình có hai nghiệm cùng dấu D. Phương trình có nghiệm kép Giải Vì ac = 1.(-1) = -1 < 0 nên phương trình có 2 nghiệm trái dấu Đáp án đúng là A Câu 2: Cho phương trình x2 – (2m + 1)x + mét vuông + m – 6 = 0. Tìm m để phương trình có 2 nghiệm âm. A. m > 2 B. m < -4 C. m > 6 D. m < -3 Giải Phương trình có 2 nghiệm cùng dấu âm khi Δ = (2m + 1)2 – 4(mét vuông + m – 6) = 4m2 + 4m + 1 – 4m2 – 4m + 24 = 25 > 0 với mọi giá trị của m(1) Suy ra m < -3 đồng thời thỏa mãn thị hiếu (1), (2) và (3) Vậy m < -3 thỏa mãn thị hiếu đề bài. Đáp án đúng là D Câu 3: Cho phương trình: x2 – 2mx + 2m – 4 = 0. Có bao nhiêu giá trị nguyên của m nhỏ hơn 2020 để phương trình có 2 nghiệm dương phân biệt. A. năm nay B. 2017 C. 2018 D. 2019 Giải Phương trình có 2 nghiệm phân biệt cùng dấu dương khi Với Δ’ > 0 ⇔ mét vuông – (2m – 4) > 0 ⇔ (mét vuông – 2m + 1) + 3 > 0 ⇔ (m – 1)2 + 3 > 0 ∀ m(1) Với P > 0 ⇔ 2m – 4 > 0 ⇔ m > 2(2) Với S > 0 ⇔ 2m > 0 ⇔ m > 0(3) Từ (1), (2), (3) ta có những giá trị m cần tìm là m > 2 Suy ra số những giá trị nguyên của m thỏa mãn thị hiếu: 2 < m < 2020 có 2017 số Đáp án đúng là B Câu 4: Cho phương trình: x2 – 2mx – 6m – 9 = 0. Tìm m để phương trình có 2 nghiệm trái dấu thỏa mãn thị hiếu x12+x22=13 Giải Phương trình có 2 nghiệm trái dấu khi: Theo Vi-et ta có: Đáp án đúng là D Câu 5: Cho phương trình: x2 – 8x + m + 5 = 0. Gọi S là tập hợp chứa toàn bộ những giá trị nguyên của m để phương trình có 2 nghiệm cùng dấu. Tính tổng toàn bộ những thành phần của S A. 30 B. 56 C. 18 D. 29 Giải Phương trình có 2 nghiệm cùng dấu khi Với Δ’ ≥ 0 ⇔ 16 – m – 5 ≥ 0 ⇔ 11-m ≥ 0 ⇔ m ≤ 11 (1) Với P > 0 ⇔ m + 5 > 0 ⇔ m > -5(2) Từ (1), (2) ta có những giá trị m cần tìm là -5 < m ≤ 11 Suy ra S = -4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9,10,11 Vậy tổng toàn bộ những thành phần của S là 56 Đáp án đúng là B Câu 6: Cho phương trình: 2×2 + (2m – 1)x + m – 1 = 0. Tìm m để phương trình có 2 nghiệm âm. A. m > 3 B. m < -1 C. m > 1 D. m < -3 Giải Phương trình có 2 nghiệm cùng dấu âm khi Từ (1), (2), (3) ta có những giá trị của m cần tìm là: m > 1 Đáp án đúng là C Câu 7: Cho phương trình mx2 + 2(m – 2)x + m – 3 = 0. Xác định m để phương trình có hai nghiệm trái dấu. A. m > 0 B. 1 < m < -1 C. 0 <m < 3 D. m < 3 Giải Để phương trình có hai nghiệm trái dấu thì m ≠ 0 và a.c < 0 Suy ra những giá trị m cần tìm là 0 < m < 3 Đáp án đúng là C Câu 8: Tìm m để phương trình mx2 – (5m – 2)x + 6m – 5 = 0 có hai nghiệm đối nhau. Giải Xét phương trình: mx2 – (5m – 2)x + 6m – 5 = 0 Để để phương trình có hai nghiệm đối nhau thì: Vậy Đáp án đúng là B Câu 9: Tìm giá trị m để phương trình 2×2 + mx + m – 3 = 0 có 2 nghiệm trái dấu và nghiệm âm có mức giá trị tuyệt đối to nhiều hơn nghiệm dương. A. 0 < m < 3 B. -1 < m < 3 C. m < 2 D. m > -3 Giải Để phương trình có hai nghiệm trái dấu thì: a.c < 0 ⇔ 2.(m-3) < 0 ⇔ m < 3 (1) Giả sử phương trình có hai nghiệm trái dấu: x1 < 0 < x2 Với m < 3 , vận dụng hệ thức Vi- ét ta có: Vì nghiệm âm có mức giá trị tuyệt đối to nhiều hơn nghiệm dương nên: |x1| > |x2| trong số đó x1 < 0; x2 > 0 nên Từ (1) và (2) suy ra 0 < m < 3 Vậy 0 < m < 3 thì phương trình có hai nghiệm trái dấu và nghiệm âm có mức giá trị tuyệt đối to nhiều hơn nghiệm dương. Đáp án đúng là A Câu 10: Tìm giá trị m để phương trình x2 – 2(m – 1)x + m – 3 = 0 có 2 nghiệm trái dấu và bằng nhau về giá trị tuyệt đối. A. m = 1 B. m = 4 C. m = 2 D. m = -3 Giải Xét phương trình: x2 – 2(m – 1)x + m – 3 = 0 có: a = 1, b = -2(m – 1), c = m – 3 Phương trình có 2 nghiệm trái dấu và bằng nhau về giá trị tuyệt đối Vậy với m = 1 thì phương trình đã cho có hai nghiệm trái dấu và bằng nhau về giá trị tuyệt đối. Đáp án đúng là A Video tương quan |
Chia sẻ
đoạn Clip Tập hợp những giá trị của m để phương trình x^2+mx-m+1=0 có hai nghiệm trái dấu ?
Một số hướng dẫn một cách rõ ràng hơn về đoạn Clip Tập hợp những giá trị của m để phương trình x^2+mx-m+1=0 có hai nghiệm trái dấu tiên tiến và phát triển nhất .
ShareLink Download Tập hợp những giá trị của m để phương trình x^2+mx-m+1=0 có hai nghiệm trái dấu miễn phí
Pro đang tìm một số trong những Chia SẻLink Tải Tập hợp những giá trị của m để phương trình x^2+mx-m+1=0 có hai nghiệm trái dấu miễn phí.
#Tập #hợp #những #giá #trị #của #để #phương #trình #x2mxm10 #có #hai #nghiệm #trái #dấu


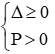
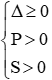
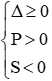
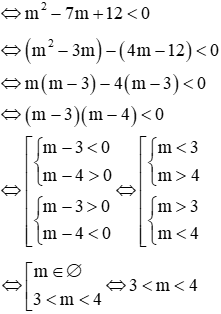
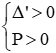
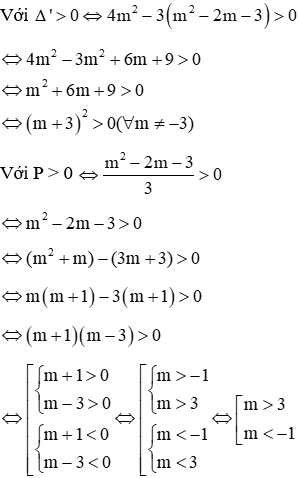
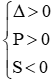
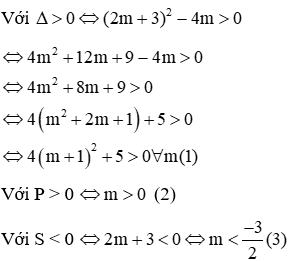

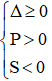
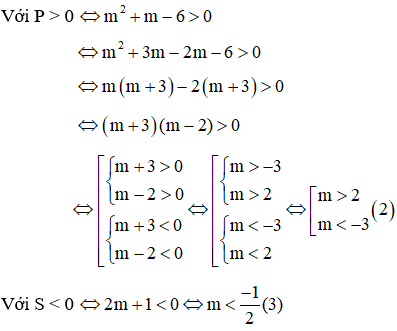
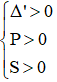
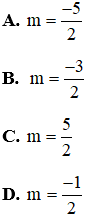
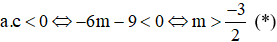
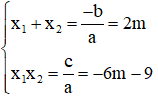
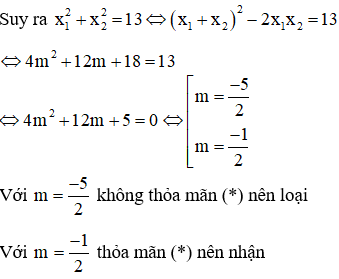
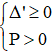

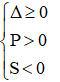
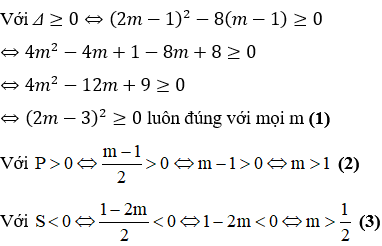
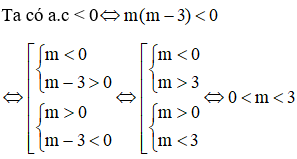
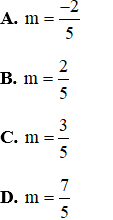
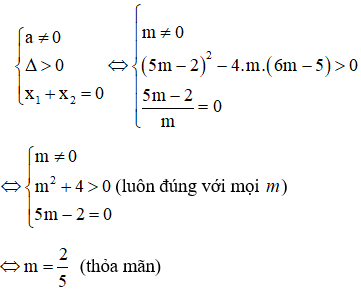
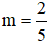 thì phương trình có hai nghiệm đối nhau.
thì phương trình có hai nghiệm đối nhau.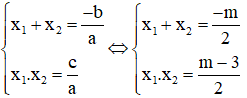
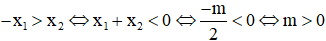 (2)
(2)