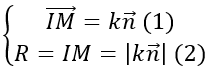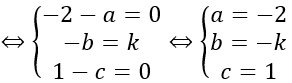Bí kíp Hướng dẫn Viết phương trình mặt cầu tiếp xúc với cả ba mặt phẳng tọa độ và trải qua điểm m(2;1;1). Chi Tiết
Bann đang tìm kiếm từ khóa Viết phương trình mặt cầu tiếp xúc với cả ba mặt phẳng tọa độ và trải qua điểm m(2;1;1). 2022-04-09 16:38:03 san sẻ Bí quyết Hướng dẫn trong nội dung bài viết một cách Chi Tiết.
Bài giảng: Cách viết phương trình mặt cầu – dạng bài cơ bản – Cô Nguyễn Phương Anh (Giáo viên VietJack) Dạng bài: Viết phương trình mặt cầu tiếp xúc với mặt phẳng (P): Ax + By + Cz + D = 0 tại điểm M (x0; y0; z0) thuộc (P) cho trước Quảng cáo Gọi I (a; b; c) ⇒ IM→=(x0 – a ; y0 – b ; z0 – c) Mặt phẳng (P) có vecto pháp tuyến n→=(A;B;C) Mặt cầu tiếp xúc với mặt phẳng (P) tại điểm M Sử dụng những Đk cho trước để tìm k ⇒ I; R Bài 1: Cho hai mặt phẳng (P) và (Q.) có phương trình (P): x – 2y + z – 1 = 0 và (Q.): 2x + y – z + 3 = 0. Viết phương trình mặt cầu có tâm nằm trên mặt phẳng (P) và tiếp xúc với mặt phẳng (Q.) tại điểm M, biết rằng M thuộc mặt phẳng (Oxy) và có hoành độ xM=1 Hướng dẫn: Điểm M thuộc mặt phẳng Oxy và có hoành độ xM=1 nên M (1; y0; 0) Mặt khác M thuộc mặt phẳng Q. nên 2. 1 + y0 + 3 = 0 ⇒ y0 =-5 ⇒ M (1; -5;0) Gọi I (a; b; c) là tâm mặt cầu ⇒ IM→=(1-a; -5-b; -c) Mặt phẳng (Q.) có vecto pháp tuyến n→=(2;1;-1) Do mặt cầu tiếp xúc với (Q.) tại điểm M nên IM→ vuông góc với mặt phẳng (Q.) ⇒ IM→= k n→ Mặt khác I thuộc mặt phẳng (P) nên tọa độ của I thỏa mãn thị hiếu phương trình mặt phẳng (P) ⇒ a-2b+c-1=0 ⇔ 1-2k+2(5+k)+k-1=0 ⇔ k=-10 Với k=-10 thì I (21; 5; -10) Bán kính của mặt cầu là R=|IM→ |=|k n→ |
Vậy phương trình mặt cầu cần tìm là: (x-21)2 +(y-5)2 +(z+10)2 =600 Quảng cáo Bài 2: Cho hai mặt phẳng (P): 2x + 3y – z + 2 = 0, (Q.): 2x – y – z + 2 = 0. Viết phương trình mặt cầu (S) tiếp. xúc với mặt phẳng (P) tại điểm A (1; -1; 1) và có tâm thuộc mặt phẳng (Q.) Hướng dẫn: Gọi I (a; b; c) là tâm của mặt cầu ⇒ IA→=(1-a; -1-b; 1-c) Mặt phẳng (P) có vecto pháp tuyến n→=(2;3;-1) Do mặt cầu tiếp xúc với (P) tại điểm A nên IA→ vuông góc với mặt phẳng (P) ⇒ IA→= k n→ Lại có I thuộc mặt phẳng (Q.) nên ta có: 2a-b-c+2=0 ⇔ 2(1-2k)+(1+3k)-1-k+2=0 ⇔ k=2 Với k = 2 thì I (-3; -7; 3) Bán kính mặt cầu: R=|IA→ |=|k n→ | Vậy phương trình mặt cầu cần tìm là: (x+3)2 +(y+7)2 +(z-3)2=56 Bài 3: Cho điểm A(2; 5; 1) và mặt phẳng (P): 6x + 3y – 2z + 24 = 0, H là hình chiếu vuông góc của A trên mặt phẳng (P). Viết phương trình mặt cầu (S) có diện tích quy hoạnh s 784π và tiếp xúc với mặt phẳng (P) tại H, sao cho điểm A nằm trong mặt cầu. Hướng dẫn: Gọi H (a; b; c). ⇒ AH→=(a-2;b-5;c-1) Mặt phẳng (P) có vecto pháp tuyến n→=(6;3;-2) Do H là hình chiếu vuông góc của A trên mặt phẳng (P) nên AH→ vuông góc với mặt phẳng (P). ⇒ AH→ =k n→ Lại có H thuộc (P) nên 6a + 3b – 2c + 24 = 0 ⇔ 6(6k+2)+3(3k+5)-2(-2k+1)+24=0 ⇔ k=-1 ⇒ H(-4;2;3) Gọi R là nửa đường kính mặt cầu. Mặt cầu (S) có diện tích quy hoạnh s là 784π ⇒ 4πR2 =784π ⇒ R=14 Gọi I (m, n, p.) là tâm mặt cầu ⇒ IH→=(-4-m;2-n;3-p.) Do mặt cầu tiếp xúc với mặt phẳng (P) tại H nên ta có Xét (*): |t n→ |=R
Với t = 2 ta có I (-16; -4; 7) Khi đó: IA ⇒ A nằm ngoài mặt cầu. Với t = – 2 ta có I (8; 8; -1) Khi đó IA ⇒ A nằm trong mặt cầu. Vậy phương trình mặt cầu cần tìm là: (x-8)2 +(y-8)2 +(z+1)2=196 Quảng cáo Bài 4: Viết phương trình của mặt cầu (S) biết (S) tiếp xúc với mặt phẳng tọa độ Oxz tại điểm M(- 2;0;1) và (S) trải qua điểm A(2;2;1) Hướng dẫn: Gọi I (a; b; c) là tọa độ tâm của mặt cầu. ⇒ IM→=(-2-a; -b;1-c) Mặt phẳng (Oxz) có vecto pháp tuyến n→=(0 ;1 ;0) Do mặt cầu (S) tiếp xúc với mặt phẳng tọa độ (Oxz) tại M nên Giải (1) : IM→= k n→ Do mặt cầu trải qua A(2; 2;1) nên IA = R Ta có : IA2 =42 +(k+2)2 =k2 +4k +20 Từ (2) ⇒ IA2 =R2 =k2 ⇒ k2 +4k +20 =k2 ⇒ k=-5 Vậy I (-2 ; 5 ; 1) và R = 5 Phương trình mặt cầu cần tìm là : (x+2)2 +(y-5)2 +(z-1)2=25 Bài giảng: Cách viết phương trình mặt cầu – dạng bài nâng cao – Cô Nguyễn Phương Anh (Giáo viên VietJack) Giới thiệu kênh Youtube VietJack phuong-phap-toa-do-trong-khong-gian.jsp Video tương quan |
Chia sẻ
đoạn Clip Viết phương trình mặt cầu tiếp xúc với cả ba mặt phẳng tọa độ và trải qua điểm m(2;1;1). ?
Một số hướng dẫn một cách rõ ràng hơn về Review Viết phương trình mặt cầu tiếp xúc với cả ba mặt phẳng tọa độ và trải qua điểm m(2;1;1). tiên tiến và phát triển nhất .
ShareLink Tải Viết phương trình mặt cầu tiếp xúc với cả ba mặt phẳng tọa độ và trải qua điểm m(2;1;1). miễn phí
Heros đang tìm một số trong những Share Link Cập nhật Viết phương trình mặt cầu tiếp xúc với cả ba mặt phẳng tọa độ và trải qua điểm m(2;1;1). miễn phí.
#Viết #phương #trình #mặt #cầu #tiếp #xúc #với #cả #mặt #phẳng #tọa #độ #và #đi #qua #điểm #m211


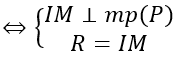
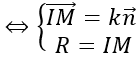
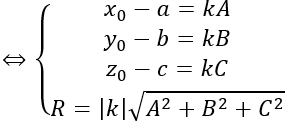
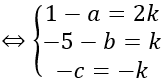
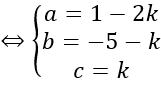
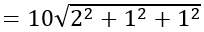 = 10√6
= 10√6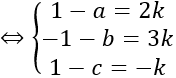
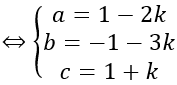
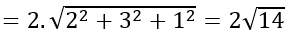
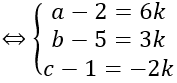
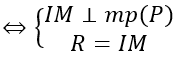
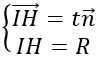
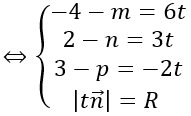
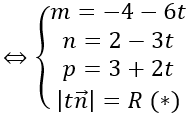
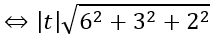 =14 ⇔ |t|=2 ⇔ t= ±2
=14 ⇔ |t|=2 ⇔ t= ±2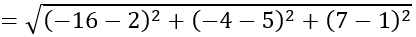 =21>R
=21>R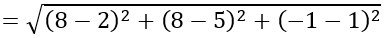 = 7<R
= 7<R