Bí kíp Hướng dẫn Bài 17 sgk toán 7 tập 1 trang 114 2022
Hero đang tìm kiếm từ khóa Bài 17 sgk toán 7 tập 1 trang 114 2022-05-16 09:09:12 san sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách 2021.
Page 2Bài 20 trang 115 – Sách giáo khoa toán 7 tập 1 Cho góc (xOy) (h.73), Vẽ cung tròn tâm (O), cung tròn này cắt (Ox, Oy) theo thứ tự ở (A,B) (1). Vẽ những cung tròn tâm (A) và tâm (B) có cùng nửa đường kính sao cho chúng cắt nhau ở điểm (C) nằm trong góc (xOy) ((2) (3)). Nối (O) với (C) (4). Chứng minh (OC) là tia phân giác của góc (xOy). 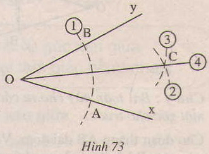 Giải: Vẽ cung tròn tâm (O), cung tròn này cắt (Ox, Oy) theo thứ tự ở (A,B) do đó (OA=OB) vì cùng bằng nửa đường kính của cung tròn Cung tròn tâm (A) và tâm (B) có cùng nửa đường kính nên ta gọi nửa đường kính là (r) (C) là giao của hai cung tròn do đó (C) thuộc cung tròn tâm (A) nên (AC=r), (C) thuộc cung tròn tâm (B) nên (BC=r) Suy ra (AC=BC) Nối (BC, AC). Xét (∆OBC) và (∆OAC) có: +) (OB=OA) +) (BC=AC) +) (OC) cạnh chung Suy ra (∆OBC = ∆OAC(c.c.c)) Nên (widehatBOC=widehatAOC) (hai góc tương ứng) Vậy (OC) là tia phân giác của góc (xOy). Bài 21 trang 115 – Sách giáo khoa toán 7 tập 1 Cho tam giác ABC, Dùng thước và compa, vẽ những tia phân giác của những góc A,B,C. Giải: Vẽ tia phân giác của góc A. Vẽ cung trong tâm A, cung tròn này cắt AB, AC theo thứ tự ở M,N. Vẽ những cung tròn tâm M và tâm N có cùng nửa đường kính sao cho chúng cắt nhau ở điểm I nằm trong góc BAC. Nối AI, ta được AI là tia phân giác của góc A. Tương tự cho cách vẽ tia phân giác của những góc B,C(Học sinh tự vẽ) 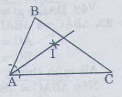 Bài 22 trang 115 – Sách giáo khoa toán 7 tập 1 Cho góc (xOy) và tia (Am) (h.74a) Vẽ cung trong tâm (O) nửa đường kính (r), cung tròn này cắt (Ox,Oy) theo thứ tự ở (B,C) Vẽ cung tròn tâm (A) nửa đường kính (r), cung này cắt kia (Am) ở (D) (h.74b). Vẽ cung tròn tâm (D) có nửa đường kính bằng (BC), cung tròn này cắt cung tròn tâm (A) nửa đường kính (r) ở (E) (h. 74c). Chứng minh rằng: (widehatDAE=widehatxOy.) 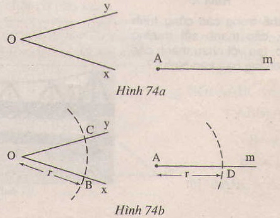
 Giải: Xét (Delta DAE) và (Delta BOC) có: +) (AD=OB(=r)) +) (DE=BC) (gt) +) (AE=OC(=r)) Suy ra (∆ DAE= ∆ BOC;(c.c.c)) Suy ra (widehatDAE=widehatBOC) (hai góc tương tứng) Mà (widehatBOC=widehatxOy.) Do đó: (widehatDAE=widehatxOy.) (điều phải chứng tỏ) Bài 23 trang 116 – Sách giáo khoa toán 7 tập 1 Cho đoạn thẳng (AB) dài (4cm) Vẽ đường tròn tâm (A) nửa đường kính (2cm) và đường tròn tâm (B) nửa đường kính (3cm), chúng cắt nhau ở (C) và (D), chứng tỏ rằng (AB) là tia phân giác của góc (CAD) Giải: 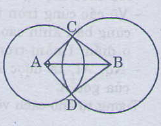 Vì (C) là giao của đường tròn tâm (A) và tâm (B) nên (AC=2cm,BC=3cm) Vì (D) là giao của đường tròn tâm (A) và tâm (B) nên (AD=2cm,BD=3cm) Do đó (AC=AD,BC=BD) Xét (∆BAC) và (∆ BAD) có: +) (AC=AD) +) (BC=BD) +) (AB) cạnh chung. Suy ra (∆ BAC= ∆ BAD(c.c.c)) Suy ra (widehatBAC) = (widehatBAD) (hai góc tương ứng) Vậy (AB) là tia phân giác của góc (CAD). Giaibaitap.me Page 3Bài 24 trang 118 – Sách giáo khoa toán 7 tập 1 Vẽ tam giác ABC biết (widehatA)= 900 AB=AC=3cm. Sau đó đo những góc B và C. Giải: Cách vẽ: – Vẽ góc (widehatxAy)=900 – Trên tia Ax vẽ đoạn thẳng AB= 3cm, – Trên tia Ay vẽ đoạn thẳng AC= 3cm, – Vẽ đoạn BC. Ta vẽ được đoạn thẳng BC. Ta đo những góc B và C ta được (widehatB)= (widehatC)=450 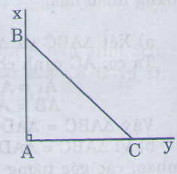 Bài 25 trang 118 – Sách giáo khoa toán 7 tập 1 Trên mỗi hình sau có những tam giác nào bằng nhau? Vì sao? 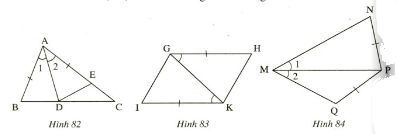 Giải: Hình 82. Xét (∆ADB) và (∆ADE) có: +) (AB=AE) (gt) +) (widehatA_1=widehatA_2), +) (AD) chung. Nên (∆ADB = ∆ADE(c.g.c)) Hình 83. Xét (∆HGK) và (∆IKG) có: +) (HG=IK) (gt) +) (widehatG)=(widehatK)(gt) +) (GK) là cạnh chung Suy ra (∆HGK = ∆IKG( c.g.c)) Hình 84. (∆PMQ) và (∆PMN) có: (MP) cạnh chung (widehatM_1)=(widehatM_2) Nhưng (MN) không bằng (MQ). Nên (PMQ) không bằng (PMN). Bài 26 trang 118 – Sách giáo khoa toán 7 tập 1 Xét bài toán: ” Cho tam giác ABC, M là trung điểm của BC, Trên tia đối của MA lấy điểm E sao cho ME=MA. Chứng minh rẳng AB//CE’. Dưới đấy là hình vẽ và giả thiết, kết luận của bài toán(h.85) 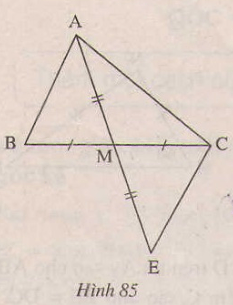 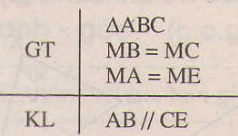
Hãy sắp xếp lại năm câu tại đây một cách hợp lý để giải bài toán trên: 1) MB = MC(gt) (widehatAMB)=(widehatEMC) (Hai góc đối đỉnh) MA= ME(Giả thiết) 2) Do đó ∆AMB=∆EMC(c.g.c) 3) (widehatMAB)=(widehatMEC)=> AB//CE(hai góc bằng nhau ở vị trí sole trong) 4) ∆AMB= ∆EMC => (widehatMAB)=(widehatMEC) (Hai góc tương ứng) 5) ∆AMB và ∆EMC có: Giải: Thứ tự sắp xếp là: 5,1,2,4,3 Bài 27 trang 119 – Sách giáo khoa toán 7 tập 1 Nêu thêm một Đk để hai tam giác trong những hình vẽ dưới đấy là hai tam giác bằng nhau theo trường hợp cạnh-góc- cạnh. a) (∆ABC= ∆ADC) (h.86); b) (∆AMB= ∆EMC) (H.87) c) (∆CAB= ∆DBA). (h.88) 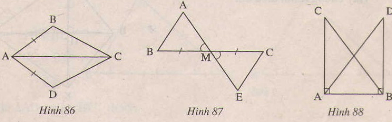 Giải: a) Bổ sung thêm (widehatBAC)=(widehatDAC). b) Bổ sung thêm (MA=ME) c) Bổ sung thêm (AC=BD) Bài 28 trang 120 – Sách giáo khoa toán 7 tập 1 Trên hình 89 có bao nhiêu tam giác bằng nhau. 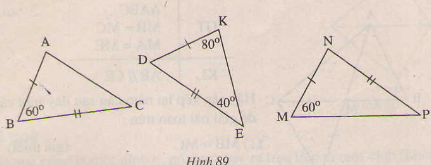 Giải: Tam giác (DKE) có: (widehatD+widehatK+widehatE=180^0) (tổng ba góc trong của tam giác). (widehatD+80^0 +40^0=180^0) (widehatD=180^0-120^0=60^0) Xét (∆ ABC) và (∆KDE) có: +) (AB=KD) (gt) +) (widehatB=widehatD=60^0) +) (BC= ED) (gt) Do đó (∆ABC= ∆KDE(c.g.c)) Giaibaitap.me Page 4
Page 5
Page 6Bài 37 trang 123 – Sách giáo khoa toán 7 tập 1 Trên mỗi hình 101,102,103 có tam giác nào bằng nhau? Vì sao? 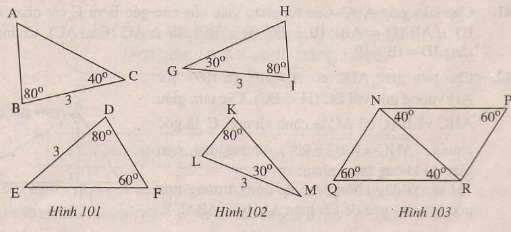 Giải: Tính những góc còn sót lại trên mỗi hình trên ta được: Áp dụng định lí tổng ba góc trong một tam giác ta có: (eqalign & widehat A = 180^0 – widehat B – widehat C = 180^0 – 80^0 – 40^0 = 60^0 cr & widehat H = 180^0 – widehat G – widehat I = 180^0 – 30^0 – 80^0 = 70^0 cr & widehat E = 180^0 – widehat D – widehat F = 180^0 – 80^0 – 60^0 = 40^0 cr & widehat L = 180^0 – widehat K – widehat M = 180^0 – 80^0 – 30^0 = 70^0 cr & widehat QNR = 180^0 – widehat NRQ – widehat RQN = 180^0 – 40^0 – 60^0 = 80^0 cr & widehat NRP = 180^0 – widehat RPN – widehat PNR = 180^0 – 60^0 – 40^0 = 80^0 cr ) – Xét (∆ABC) và (∆FDE) (Hình 101) +) (widehatB = widehatD) +) (BC=DE) +) (widehatC=widehatE) Suy ra (∆ABC=∆FDE) (g.c.g) – Xét (∆NQR) và (∆RPN) (Hình 103) +) (widehatQNR=widehatNRP) ((=80^0)) +) (NR) là cạnh chung. +) (widehatNRQ=widehatRNP) ((40^0)) Suy ra (∆NQR=∆RPN) (g.c.g) – Xét (Delta HIG) và (Delta LKM) (Hình 102) (eqalign& + ),,GI = ML cr & + ),,widehat G = widehat M cr & + ),,widehat I = widehat K cr ) Ta có: (widehat G,; widehat I) cùng kề với cạnh (GI), còn (widehat M ) kề với cạnh (ML) nhưng ( widehat K) không kề với cạnh (ML) nên (Delta HIG) không bằng (Delta LKM). Bài 38 trang 124 – Sách giáo khoa toán 7 tập 1 Trên hình 104 ta có AB//CD, AC//BD. Hãy chứng tỏ rằng AB=CD,AC=BD. Giải. 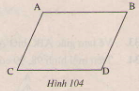 Vẽ đoạn thẳng AD. ∆ADB và ∆DAC có: (widehatA_1)= (widehatD_1)(so le trong AB//CD) AD là cạnh chung. (widehatA_2)=(widehatD_2)(So le trong, AC//BD) Do đó ∆ADB=∆DAC(g.c .g) Suy ra: AB=CD, BD=AC Bài 39 trang 124 – Sách giáo khoa toán 7 tập 1 Trên mỗi hình 105,106,108 những tam giác vuông nào bằng nhau? Vì sao? 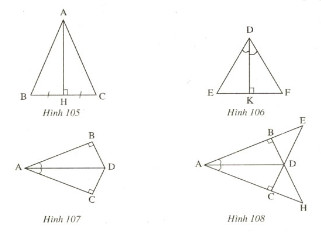 Giải: Hình 105 (∆ABH) và (∆ACH) có: +) (BH=CH) (gt) +) (widehatAHB=widehatAHC) (góc vuông) +) (AH) là cạnh chung. vậy (∆ABH=∆ACH) (c.g.c) Hình 106 (∆DKE) và (∆DKF) có: +) (widehatEDK=widehatFDK)(gt) +) (DK) là cạnh chung. +) (widehatDKE=widehatDKF) (góc vuông) Vậy (∆DKE=∆DKF) (g.c.g) Hình 107 Theo định lí tổng ba góc trong một tam giác ta có: (eqalign & widehat ABD + widehat BDA + widehat DAB = 180^0 cr & widehat ACD + widehat CDA + widehat DAC = 180^0 cr ) Mặt khác ta có: (eqalign & widehat DAB = widehat DAC,,,(gt) cr & widehat ABD = widehat ACD = 90^0 cr ) Nên (widehat BDA = widehat CDA) Xét (∆ABD) và (∆ACD) có: +) (widehat DAB = widehat DAC,,,(gt)) +) (AD) cạnh chung +) (widehat BDA = widehat CDA) (cmt) (∆ABD=∆ACD) (g.c.g) Hình 108 Theo định lí tổng ba góc trong một tam giác ta có: (eqalign& widehat ABD + widehat BDA + widehat DAB = 180^0 cr & widehat ACD + widehat CDA + widehat DAC = 180^0 cr ) Mặt khác ta có: (eqalign& widehat DAB = widehat DAC,,,(gt) cr & widehat ABD = widehat ACD = 90^0 cr ) Nên (widehat BDA = widehat CDA) Xét (∆ABD) và (∆ACD) có: +) (widehat DAB = widehat DAC,,,(gt)) +) (AD) cạnh chung +) (widehat BDA = widehat CDA) (cmt) (∆ABD=∆ACD) (g.c.g) Suy ra: (BD=CD) (hai cạnh tương ứng ) (AB=AC) (hai cạnh tương ứng ) Xét (∆DBE) và (∆DCH) +) ( widehat EBD = widehat HCD = 90^0 ) +) (BD=CD) (cmt) +) (widehat BDE = widehat CDH) (đối đỉnh) (∆DBE=∆DCH) (g.c.g) Xét (∆ABH) và (∆ACE ) +) (widehat A) chung +) (AB=AC) (cmt) +) (widehat ABH = widehat ACE = 90^0) (∆ABH=∆ACE ) (g.c.g) Bài 40 trang 124 – Sách giáo khoa toán 7 tập 1 Cho tam giác ABC(AB≠AC), tia Ax trải qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax(E ∈ Ax, F∈Ax ). So sánh độ dài BE và CF/ Giải Hai tam giác vuông BME, CMF có: BM=MC(gt) (widehatBME)=(widehatCMF)(đối đỉnh) Nên ∆BME=∆CMF(cạnh huyền- góc nhọn). Suy ra BE=CF. Giaibaitap.me Page 7Bài 41 trang 124 – Sách giáo khoa toán 7 tập 1 Cho tam giác (ABC), những tia phân giác của những góc (B) và (C) cắt nhau ở (I). Vẽ (ID) (perp) (AB) ((D) nằm trên( AB)), (IE) (perp) (BC) ((E) thuộc (BC) ), (IF) vuông góc với (AC) ((F) thuộc (AC)) CMR: (ID=IE=IF). Giải: 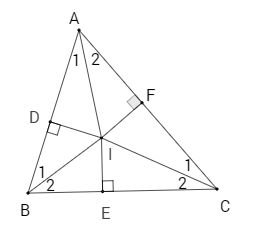 Xét hai tam giác vuông (BID) và (BIE) có: +) (BI) là cạnh chung +) (widehatB_1=widehatB_2) ( vì (BI) là phân giác góc B) Suy ra (∆BID=∆BIE) (cạnh huyền – góc nhọn) Suy ra (ID=IE) (hai cạnh tương ứng) (1) Xét hai tam giác vuông (CIF) và (CIE) có: +) (CI) cạnh chung +) (widehatC_1=widehatC_2) ( vì (CI) là phân giác góc C) Suy ra (∆CIF=∆CIE) (cạnh huyền – góc nhọn). Suy ra: (IE =IF) (hai cạnh tương ứng) (2) Từ (1) và (2) suy ra: (ID=IE=IF). loigiaihay.com Bài 42 trang 124 – Sách giáo khoa toán 7 tập 1 Cho tam giác ABC có (widehatA)= 900, kẻ AH vuông góc với BC(H∈BC). C ác tam giác AHC và BAC có AC là cạnh chung, là góc chung, (widehatAHC)=(widehatBAC)=900, nhưng hai tam giác không bằng nhau. Tại sao ở đây không vận dụng trường hợp góc cạnh góc để kết luận ∆AHC= ∆BAC? Giải: 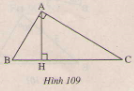 Các tam giác AHC và BAC có: AC là cạnh chung (widehatC) góc chung. (widehatAHC)=(widehatBAC)=900, Nhưng hai tam giác không bằng nhau vì góc AHC không phải là góc kề với AC. Bài 43 trang 125 – Sách giáo khoa toán 7 tập 1 Cho góc xOy khác góc bẹt. Lấy những điểm A,B thuộc tia Ox sao cho OA<OB. Lấy những điểm C,D thuộc tia Oy sao cho OC=OA, OD=OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng: a) AD=BC; b) ∆EAB=∆ECD; c )OE là tia phân giác của xOy. Giải: a) ∆OAD và ∆OCB có: OA= OC(gt) (widehatAOD)=(widehatCOB)(=(widehatA)) OD=OB(gt) Nên ∆OAD=∆OCB(c.g.c) suy ra AD=BC. b) ∆OAD=∆OCB(cmt) Suy ra: (widehatD)= (widehatB) (widehatA_1)=(widehatC _1) => (widehatA _2)=(widehat C _2) Do đó ∆AOE = ∆OCE(c .c.c) suy ra: (widehat OAE)=(widehat COE) vậy OE là tia phân giác của xOy. b) ∆AEB= ∆CED(câu b) => EA=EC. ∆OAE và ∆OCE có: OA=OC(gt) EA=EC(cmt) OE là cạnh chung. Nên ∆OAE=∆(OCE)(c .c.c) suy ra: (widehat AOE)=(widehat C OE) vậy OE là tia phân giác của góc xOy. Bài 44 trang 125 – Sách giáo khoa toán 7 tập 1 Cho tam giác ABC có (widehat B)=(widehat C). Tia phân giác của góc A cắt BC tại D. Chứng minh rằng. a) ∆ADB=∆ADC. b) AB=AC. Giải: 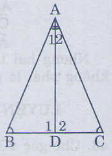 a) ∆ADB và ∆ ACD có: (widehat B)=(widehat C)(gt) (1) (widehat A_1)=(widehat A_2)(AD là tia phân giác) Nên (widehat D_1)=(widehat D_2) AD cạnh chung. Do đó ∆ADB=∆ADC(g.c.g) b) ∆ADB=∆ADC(câu a) Suy ra AB=AC . Bài 45 trang 125 – Sách giáo khoa toán 7 tập 1 Đố: Cho 4 đoạn thẳng AB,BC,CD,DA trên giấy tờ kẻ ô vuông như ở hinh 110. Hãy lập luận để lý giải: a) AB=CD, BC=AD; b) AB//CD. 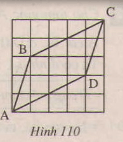 Giải: ∆AHB và ∆ CKD có: HB=KD. (widehat AHB)=(widehat CKD) AH=Ck Nên ∆ AHB = ∆ CKD(c.g.c) suy ra AB=CD. tương tự ∆ CEB = ∆ AFD(c.g.c) suy ra BC=AD. b) ∆ABD và ∆CDB có: AB=CD(câu a) BC=AD(câu a) BD chung. Do đó ∆ABD=∆CDB(c.c .c) Suy ra (widehat ABD)=(widehat CDB) Vậy AB // CD( hai góc so le trong bằng nhau) Giaibaitap.me Page 8
Page 9
Page 10
Page 11
Page 12
Page 13
Page 14Bài 67 trang 140 sgk toán 7 tập 1 Điền dấu “x” vào chỗ trống (…) một cách thích hợp:
Hướng dẫn làm bài:
Bài 68 trang 141 sgk toán 7 tập 1 Các tính chất tại đây được suy ra trực tiếp từ định lí nào? a) Góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó. b) Trong một tam giác vuông, hai góc nhọn phụ nhau. c) Trong một tam giác đều, những góc bằng nhau. d) Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều. Hướng dẫn làm bài: Các tính chất ở những câu (a); (b) được suy ra từ định lí: “Tổng ba góc của một tam giác bằng nhau bằng 1800”. Tính chất ở câu (c) được suy ra từ định lí: “Trong tam giác cân, hai góc ở đáy bằng nhau”. Tính chất ở câu (d) được suy ra từ định lí: “Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân”. Bài 69 trang 141 sgk toán 7 tập 1 Cho điểm A nằm ngoài đường thẳng a. Vẽ cung tròn tâm A cắt đường thẳng a ở B và C. Vẽ những cung tròn tâm B và tâm C có nửa đường kính sao cho chúng cắt nhau tại một điểm khác A, gọi điểm đó là D. Hãy lý giải vì sao AD vuông góc với đường thẳng a. Hướng dẫn làm bài: 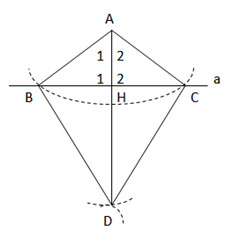 ∆ABD và ∆ACD có: AB = AC (gt) DB = DC (gt) AD cạnh chung. Nên ∆ABD = ∆ACD (c.c.c) => (widehat A_1 = widehat A_2) (1) Gọi H là giao điểm của AD và a. ∆AHB và ∆AHC có: AB = AC (gt) (widehat A_1 = widehat A_2) (1) AH cạnh chung. Nên ∆AHB = ∆AHC (c.g.c) Suy ra: (widehat H_1 = widehat H_2) Ta lại sở hữu: (widehat H_1 + widehat H_2 = 180^0 Rightarrow widehat H_1 = widehat H_2 = 90^0) Vậy AD ⊥ a. Bài 70 trang 141 sgk toán 7 tập 1 Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN. a) Chứng minh rằng tam giác AMN là tam giác cân. b) Kẻ BH ⊥ AM (H AM), kẻ CK ⊥ AN (K. Chứng minh rằng BH = CK. c) Chứng minh rằng AH = AK. d) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao ? e) Khi (widehat BAC = 60^0) và BM = CN = BC, hãy tính số đo những góc của tam giác AMN và xác lập dạnh của tam giác OBC. Hướng dẫn làm bài: 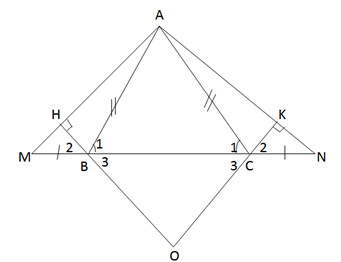 a) ∆ABC cân, suy ra (widehat B_1 = widehat C_1) (Rightarrow widehat ABM = widehat ACN) ∆ABM và ∆CAN có: AB = AC (gt) (widehat ABM = widehat ACN) BM = ON (gt) Suy ra (widehat M = widehat N) =>∆AMN là tam giác cân ở A. b) Hai tam giác vuông ∆BHM và ∆CKN có : BM = CN (gt) (widehat M = widehat N) (CM từ câu a) Nên ∆BHM = ∆CHN (cạnh huyền, góc nhọn) Suy ra BH = CK. c) Theo câu (a) ta có tam giác AMN cân ở A nên AM = AN (*) Theo câu b ta có ∆BHM = ∆CKN nên suy ra HM = KN (**). Do đó AH = AM – HM = AN – KN (theo (*) và (**)) = AK Vậy AH = AK. d) ∆BHM = ∆CKN suy ra (widehat B_2 = widehat C_2) Mà (widehat B_2 = widehat B_3;widehat C_2 = widehat C_3) (đối đỉnh) Nên (widehat B_3 = widehat C_3) . Vậy ∆OBC là tam giác cân. e) Khi (widehat BAC = 60^0) và BM = CN = BC. +Tam giác cân ABC có (widehat BAC = 60^0) nên là tam giác đều. Do đó: AB = BC = AC = BM = CN (widehat ABM = widehat ACN = 120^0) (cùng bù với 600) ∆ABM cân ở B nên (widehat M = widehat BAM = 180^0 – 120^0 over 2 = 30^0) . Suy ra (widehat ANM = widehat AMN = 30^0) . Và (widehat MAN = 180^0 – left( widehat AMN + widehat ANM right) = 180^0 – 2.30^0 = 120^0) Vậy ∆AMN có (widehat M = widehat N = 30^0;widehat A = 120^0.) +∆BHM có: (widehat M = 30^0) nên (widehat B_2 = 60^0) (hai góc phụ nhau) Suy ra (widehat B_3 = 60^0) Tương tự (widehat C_3 = 60^0) Tam giác OBC có (widehat B_3 = widehat C_3 = 60^0) nên tam giác OBC là tam giác đều. (Tam giác cân có một góc bằng 600 nên là tam giác đều). Giaibaitap.me Page 15
Page 16
Page 17Bài 5 trang 11 sgk toán 7 – tập 2 Trò chơi toán học: Thống kê ngày, tháng, năm sinh của những bạn trong lớp và những bạn có cùng tháng sinh thì xếp thành một nhóm. Điền kết quả thu được theo mẫu ở bảng 10:  Hướng dẫn giải: Căn cứ vào tháng sinh của những bạn trong lớp của tớ để tìm tần số tương ứng. Sau đó điền kết quả vào bảng. Chẳng hạn khảo sát tháng, năm sinh của một lớp tại một trường trung học cơ sở, ta có bảng thống kê số liệu ban sơ như sau: 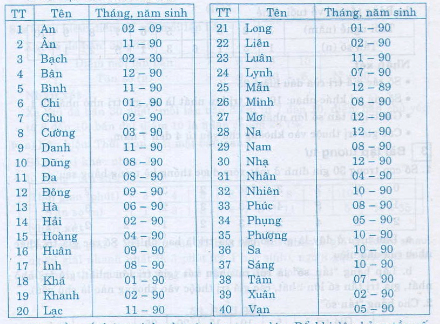 Tìm tần số tháng sinh của những bạn trong lớp. Để khi lập bảng tần số không nhần lẫn, ta kê ra toàn bộ những giá trị rất khác nhau của tín hiệu (những tháng từ là một trong những – 12) lần lượt đọc tháng sinh từ trên xuống. Mỗi lần gặp tháng nào ta gạch vào cột tháng đó một vạch. Sau khi vạch xong, ta đếm số vạch của mỗi cột để ghi thành bảng “tần số” như sau: 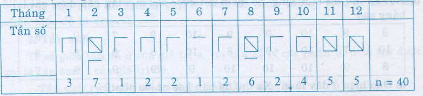 . Bài 6 trang 11 sgk toán 7 – tập 2 Kết quả khảo sát về con của 30 mái ấm gia đình thuộc một thôn được cho trong bảng 11: 
a) Dấu hiệu cần tìm hiểu ở đấy là gì ? Từ đó lập bảng “tần số”. b) Hãy nêu một số trong những nhận xét từ bảng trên về số lượng con của 30 mái ấm gia đình trong thôn (số con của những mái ấm gia đình trong thôn đa phần thuộc vào lúc nào ? Số mái ấm gia đình đông con, tức 3 con trở lên chỉ chiếm khoảng chừng một tỉ lệ bao nhiêu ?) Hướng dẫn giải: a) Dấu hiệu cần tìm hiểu: Số con của mỗi mái ấm gia đình. Bảng “tần số” về số con  b) Nhận xét: – Số con của mỗi mái ấm gia đình đa phần thuộc vào lúc từ 0 đến 4 người con. – Số mái ấm gia đình đông con (từ 3 người con trở lên) là 7 chiếm tỉ lệ: 7/30 tức 23,3%. Bài 7 trang 11 sgk toán 7 – tập 2 Tuổi nghề (tính theo năm) của một số trong những công nhân trong một phân xưởng được ghi lại ở bảng 12:  a) Dấu hiệu ở đấy là gì ? Số những giá trị là bao nhiêu ? b) Lập bảng “tần số” và rút ra một số trong những nhận xét (số những giá trị của tín hiệu, số những giá trị rất khác nhau, giá trị lớn số 1, giá trị nhỏ nhất, giá trị có tần số lớn số 1, những giá trị thuộc vào lúc nào đa phần). Hướng dẫn giải: a) Dấu hiệu: tuổi nghề của công nhân trong một phân xưởng. Số những giá trị: 25. b) Bảng tần số về tuổi nghề 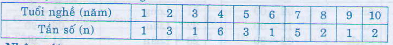 Nhận xét:
Bài 8 trang 12 sgk toán 7 – tập 2 Một xạ thủ thi bắn súng. Số điểm đạt được sau mỗi lần bắn được ghi lại ở bảng 13:  a) Dấu hiệu ở đấy là gì ? Xạ thủ đã bắn bao nhiêu phát ? b) Lập bảng “tần số” và rút ra một số trong những nhận xét. Hướng dẫn giải: a) Dấu hiệu: điểm số của mỗi lần bắn. Xạ thủ đã bắn: 30 phát  Nhận xét: Xạ thủ đã bắn 30 phát, mỗi lần bắn điểm từ 7 đến 10, điểm bắn đa phần từ 8 đến 10, bắn đạt điểm 10 là 8 lần chiếm 26,7%. Bài 9 trang 12 sgk toán 7 – tập 2 Thời gian giải một bài toán (tính theo phút) của 35 học viên được ghi trong bảng 14: 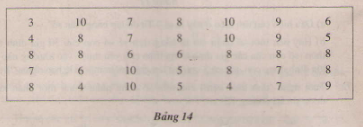 a) Dấu hiệu ở đấy là gì ? Số những giá trị là bao nhiêu ? b) Lập bảng “tần số” và rút ra một số trong những nhận xét. Hướng dẫn giải: a) Dấu hiệu: Thời gian giải một bài toán Số giá trị rất khác nhau: 8 b) Bảng “tần số”  Nhận xét Thời gian giải 1 bài toán của 35 học viên chỉ nhận 8 giá trị rất khác nhau, người giải nhanh nhất có thể là 3 phút (có một học viên), người giải chậm nhất là 10 phút, thời hạn giải xong đa phần từ 6 đến 8 phút. Giaibaitap.me Page 18
Page 19
Page 20
Page 21
Page 22Bài 1 trang 26 sgk toán 7 – tập 2 Hãy viết những biểu thức đại số biểu thị: a) Tổng của x và y; b) Tích của x và y; c) Tích của tổng x và y với hiệu của x và y. Hướng dẫn giải: a) Tổng của x và y là x + y b) Tích của x và y là xy c) Tích của tổng x và y với hiệu của x và y với hiệu của x và y là (x + y) (x – y). Bài 2 trang 26 sgk toán 7 – tập 2 Viết biểu thức đại số biểu thị diện tích quy hoạnh s hình thang có đáy lớn là a, đáy nhỏ là b, đường cao là h (a, b và h có cùng cty chức năng đo). Hướng dẫn giải: Hình thang có đáy lớn là a, đáy nhỏ là b, đường cao là h thì biểu thức tính diện tích quy hoạnh s hình thang là: (frac(a+b)h2) hoặc (frac12) (a + b)h hoặc (a + b)h : 2. Bài 3 trang 26 sgk toán 7 – tập 2 Dùng bút chì nối những ý 1), 2), …, 5) với a), b), …, c) sao cho chúng có cùng ý nghĩa (ví như nối ý 1) với e)) :  Hướng dẫn giải: Ý 1) đã cho là x – y được đọc là hiệu của x và y. Đem so sánh với những ý cần nối kết thì ta chọn ý e) vì chúng có cùng ý nghĩa. Làm tương tự cho những câu còn sót lại ta được kết quả sau: 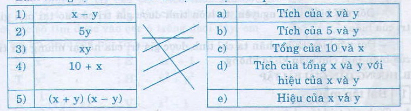 . Bài 4 trang 27 sgk toán 7 – tập 2 Một ngày ngày hè, buổi sáng nhiệt độ là t độ, giữa trưa nhiệt độ tăng thêm x độ so với buổi sáng, buổi chiều lúc mặt trời lặn nhiệt độ lại giảm sút y độ so với giữa trưa. Hãy viết biểu thức đại số biểu thị nhiệt độ lúc mặt trời lặn của ngày đó theo t, x, y. Hướng dẫn giải: Biểu thức đại số biểu thị nhiệt độ lúc mặt trời lặn là: t + x – y. Bài 5 trang 27 sgk toán 7 – tập 2 Một người hưởng mức lương là a đồng trong một tháng. Hỏi người đó nhận được bao nhiêu tiền, nếu: a) Trong một quý lao động, người đó bảo vệ bảo vệ an toàn đủ ngày công và thao tác có hiệu suất cao nên được thưởng thêm m đồng ? b) Trong hai quý lao động, người đó bị trừ n đồng (n < a) vì nghỉ một ngày công không phép ? Hướng dẫn giải: a) Một quý có 3 tháng do đó trong một quý người đó lãnh được 3a đồng. Vì đảm bảo đủ ngày công và thao tác có hiệu suất cao cực tốt nên trong quý người này được hưởng thêm m đồng. Vậy trong một quý người này được lãnh toàn bộ là 3a + m (đồng). b) Trong hai quý lao động (6 tháng) người đó lãnh được 6a (đồng) tiền lương. Theo đề bài, trong quý lao động người đó chỉ từ lãnh được 6a – n (đồng). Giaibaitap.me Page 23Bài 6 trang 28 sgk toán 7 – tập 2 Đố: Trao Giải toán học Việt Nam (dành riêng cho giáo viên và học viên phổ thông) mang tên nhà toán học nổi tiếng nào ?  (Quê ông ở thành phố Hà Tĩnh. Ông là người thầy của nhiều thế hệ những nhà toán học việt nam trong thế kỉ XX). Hãy tính giá trị của những biểu thức sau tại x = 3, y = 4 và z = 5 rồi viết những chữ tương ứng với những số tìm kiếm được vào những ô trống tại đây, em sẽ vấn đáp được vướng mắc trên: N x2 ; Ê 2×2 +1; T y2 ; H x2 + y2 Ă (frac12)(xy + z); V z2 – 1; L x2 – y2 I Biểu thức biểu thị chu vi của hình chữ nhật có những cạnh là y, z. M Biểu thức biểu thị cạnh huyền của tam giác vuông có hai cạnh góc vuong x, y. 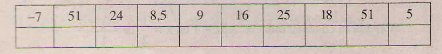 Hướng dẫn giải: Lần lượt tính giá trị biểu thức tại x = 3, y = 4, z = 5; ta được N: x2 = 32 = 9; T: y2 = 42 =16; Ă: (frac12)(xy + z) = (frac12)(3.4 +5)= 8,5; L: x2 – y2 = 32 – 42 = -7; M: t2 = x2 + y2 = 32 + 42 =25 → t = 5 (t là độ dài cạnh huyền); Ê: 2×2 +1 = 2,52 + 1 = 51; H: x2 + y2= 32 + 42 =25; V: z2 – 1= 52 – 1 = 24; I: 2(y + z) = 2(4 +5) =18; Điền vào ô trống  Vậy phần thưởng toán học Việt Nam mang tên nhà toán học nổi tiếng Lê Văn Thiêm. Bài 7 trang 29 sgk toán 7 – tập 2 Tính giá trị những biểu thức sau tại m = -1 và n = 2: a) 3m – 2n; b) 7m + 2n – 6. Hướng dẫn giải: a) Thay m = -1 và n = 2 ta có: 3m – 2n = 3(-1) -2.2 = -3 – 4 = -7 b) Thay m = -1 và n = 2 ta được 7m + 2n – 6 = 7.(-1) + 2.2 – 6 = -7 + 4 – 6 = -9. Bài 8 trang 29 sgk toán 7 – tập 2 Đố: Ước tính số gạch cần mua ? Giả sử mái ấm gia đình em cần lát một nền nhà hình chữ nhật bằng gạch hình vuông vắn có cạnh là 30 cm. Hãy đo kích thước nền nhà đó rồi ghi vào ô trống trong bảng sau:  Hướng dẫn giải: Như bài thực hành thực tế, bằng phương pháp đo chiều dài, chiều rộng của lớp học, thư viện, hội trưởng, phòng bộ môn … rồi tính theo công thức và điền vào bảng 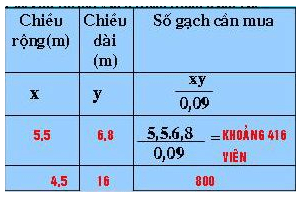 Bài 9 trang 29 sgk toán 7 – tập 2 Tính giá trị của biểu thức x2y3 + xy tại x = 1 và y = (frac12). Hướng dẫn giải: Thay x = 1 và y = (frac12) vào biểu thức ta được: x2y3 + xy = 13. ((frac12) )3 + 1. ((frac12)) = 1. (frac18) + (frac12) = (frac18) + (frac12) = (frac1+48) = (frac58) Vậy giá trị của biểu thức x2y3 + xy tại x = 1 và y = (frac12) là (frac58). Giaibitap.me Page 24Bài 10 trang 32 sgk toán 7 – tập 2 Bạn Bình viết ba ví dụ về đơn thức như sau: (5 – x)x2; -(frac59)x2y; -5. Em hãy kiểm tra xem bạn viết đã đúng chưa. Hướng dẫn giải: Bạn Bình đã viết đúng 2 đơn thức đó là -(frac59)x2y; -5. Biểu thức (5 – x)x2 = 5×2 – x3 không là đơn thức vì trong biểu thức có chứa phép trừ. Bài 11 trang 32 sgk toán 7 – tập 2 Trong những biểu thức sau, biểu thức nào là đơn thức ? a) (frac25) + x2y; b) 9x2yz; c) 15,5; d) 1 – (frac59)x3. Hướng dẫn giải: Theo định nghĩa đơn thức, những biểu thức sau là đơn thức b) 9x2yz; c) 15,5; Các biểu thức a) (frac25) + x2y; d) 1 – (frac59)x3; không phải là đơn thức vì chúng có chứa phép cộng hoặc phép trừ. Bài 12 trang 32 sgk toán 7 – tập 2 a) Cho biết phần thông số, phần biến của mỗi đơn thức sau: 2,5x2y; 0,25x2y2. b) Tính giá trị của mỗi đơn thức trên tại x = 1 và y = -1. Hướng dẫn giải: a) Đơn thức 2,5x2y có thông số là 2,5; phần biến là x2y. Đơn thức 0,25x2y2 có thông số là 0,25; phần biến là x2y2. b) Thay x = 1 và y = -1 vào đơn thức 2,5x2y ta được 2,5x2y = 2,5.12(-1) = -2,5 Vậy đơn thức 2,5x2y có mức giá trị bằng -2,5 tại x = 1; y = -1. Với đơn thức 0,25x2y2 ta được: 0,25x2y2 = 0,25 . 12 . (-1)2 = 0,25 . 1 . 1 = 0,25 Vậy đơn thức 0,25x2y2 có mức giá trị bằng 0,25 tại x = 1; y = -1. Bài 13 trang 32 sgk toán 7 – tập 2 Tính tích những đơn thức sau rồi tìm bậc của đơn thức thu được: a) -(frac13)x2y và 2xy3; b) (frac14)x3y và -2x3y5. Hướng dẫn giải: (-(frac13)x2y) (2xy3) = (-(frac13) . 2) (x2 . x) (y . y3) = (frac-23) x3 y4; Đơn thức tích có bậc 7. b) ((frac14)x3y) (-2x3y5) = – (frac12)x6 y6; Đơn thức tích có bậc 12. Bài 14 trang 32 sgk toán 7 – tập 2 Hãy viết những đơn thức với biến x, y và có mức giá trị bằng 9 tại x = -1 và y = 1. Hướng dẫn giải: Có nhiều cách thức viết, đơn thức đơn thuần và giản dị nhất là 9x2y. Tổng quát: x2ny2m+1 (m, n ∈ N*). VD : +) -9xy ; -9x³y ; -9xy³ ; -9xy² ; v.v…Tổng quát của trường hợp này là : (-9.x^(2k + 1)).yⁿ (Tức là số mũ của x phải lẽ,số mũ của y tùy ý ; k,n Є N ) +) 9x²y ; 9x²y² ; (9x^4).y³ ; v.v…Tổng quát của trường hợp này là : ( -9.x^(2k)).yⁿ (Tức là số mũ của x chẵn,số mũ của y tùy ý ; k,n Є N ) Giaibaitap.me Page 25
Page 26
|
đoạn Clip Bài 17 sgk toán 7 tập 1 trang 114 ?
Một số hướng dẫn một cách rõ ràng hơn về Review Bài 17 sgk toán 7 tập 1 trang 114 tiên tiến và phát triển nhất .
Share Link Down Bài 17 sgk toán 7 tập 1 trang 114 miễn phí
Người Hùng đang tìm một số trong những ShareLink Tải Bài 17 sgk toán 7 tập 1 trang 114 miễn phí.
#Bài #sgk #toán #tập #trang
