Bí quyết về Phương pháp giải cực trị hàm số 2021
Bạn đang tìm kiếm từ khóa Phương pháp giải cực trị hàm số 2022-05-15 19:57:10 san sẻ Bí quyết Hướng dẫn trong nội dung bài viết một cách Chi Tiết.
Tất tần tật những dạng bài tập cực trị của hàm số lớp 12 sẽ tiến hành “xử” nhanh gọn bằng bộ công thức sau của CCBook. Teen 2K1 nhớ lưu lại và nỗ lực làm nhiều bài tập để vận dụng những công thức tính nhanh đó một cách thật linh hoạt nhé.
 Tổng hợp những công thức giải toán cực trị lớp 12 nhanh nhất có thể Công thức giải bài tập cực trị của hàm số lớp 12 siêu nhanhNếu chỉ giải những bài tập cực trị hàm số bằng phương pháp tự luận thường thì, những em sẽ không còn thể đưa ra đáp án trong thời hạn ngắn. Trong khi đó đề thi trắc nghiệm môn Toán 50 câu mà chỉ được làm trong 90 phút. Nghĩa là những em sẽ chỉ có hơn 1 phút để làm một câu. Chưa tính đến những vướng mắc khó cần thời hạn nhiều hơn thế nữa. Vì vậy, học phương pháp và công thức tính nhanh là yếu tố cực kỳ thiết yếu. Sau đây CCBook sẽ gửi đến những em bộ công thức giải nhanh những dạng bài tập cực trị của hàm số lớp 12. Tổng hợp kiến thức và kỹ năng Hóa học lớp 10 trọng tâm nhất Dạng nội dung bài viết phương trình đường thẳng qua điểm cực lớn, cực tiểuMới đầu khi đọc vướng mắc của bài toán, chứng minh và khẳng định quá nhiều học viên nghĩ rằng đấy là dạng bài phức tạp, cần nhiều thời hạn để giải. Nhưng thực ra, những em trọn vẹn trọn vẹn có thể đưa ra đáp án trong vòng gần đầy 1 phút nhờ những công thức sau: – Đối với hàm số: y = ax³ + bx² + cx + d Phương trình đường thẳng trải qua hai điểm cực trị (Δ): g(x). 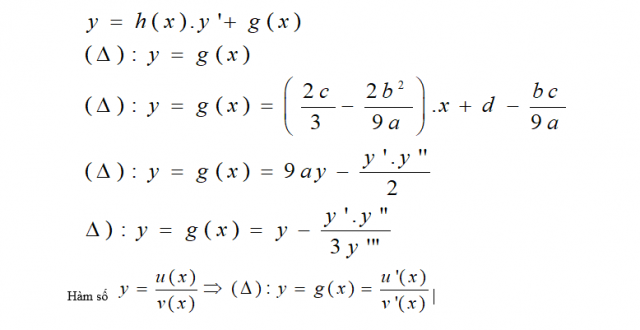 Các công thức tính nhanh bài tập cực trị của hàm số lớp 12 hàm bậc 3Đối với dạng hàm số bậc ba, teen 2K1 sẽ cần nhớ những công thức cốt lõi sau. Những công thức này đều tương hỗ những em làm bài tập rất nhanh rất đúng chuẩn. – Hàm số không tồn tại cực trị: Δy’ ≤ 0 – Hàm số có cực trị: Δy’ > 0. – A, B là hai điểm cực trị trên đồ thị:  – Hàm số đạt cực trị tại x0 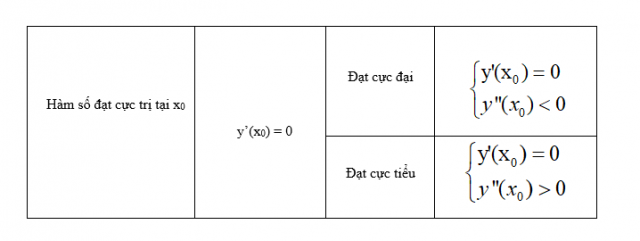 – Hàm số có hai cực trị: 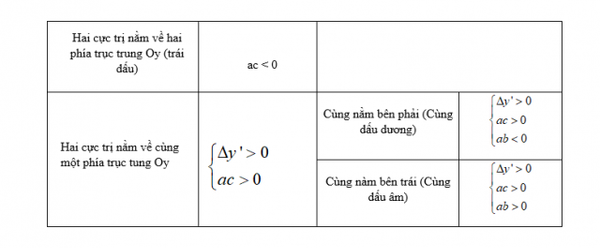 Ngoài những công thức tính nhanh trên, teen 2K1 cũng trọn vẹn có thể sử dụng máy tính cầm tay để tiết kiệm ngân sách tối đa thời hạn làm bài. Hãy tìm hiểu thêm: Xong ngay bài tập cực trị hàm số lớp 12 bằng máy tính cầm tay Giải nhanh bài tập cực trị của hàm số lớp 12 hàm trùng phương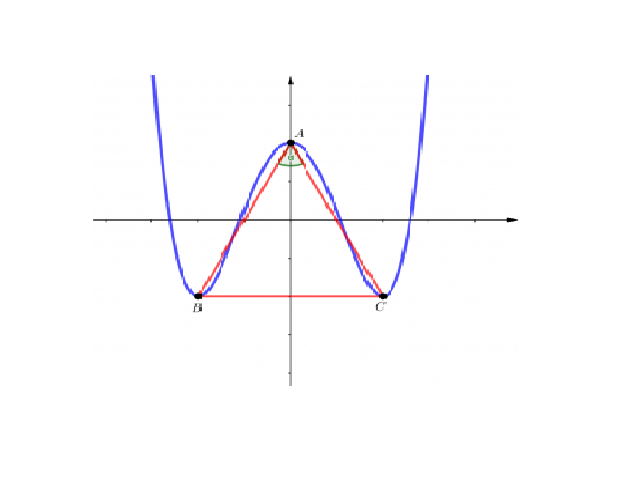 Hàm trùng phương: y = x4 + bx2 + c 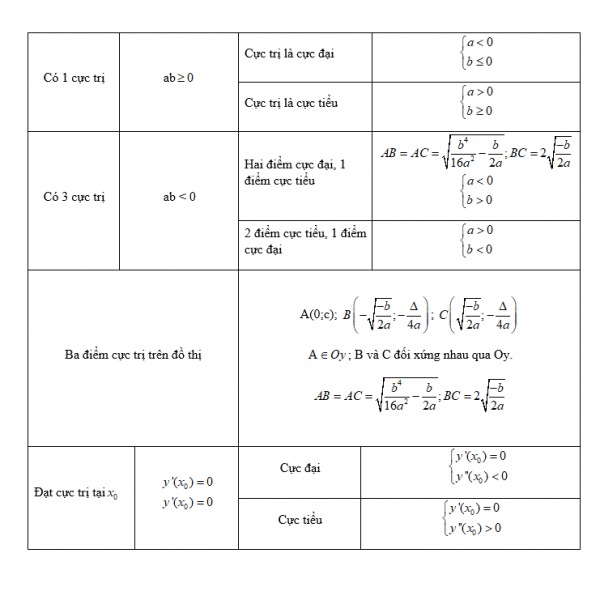 Bên cạnh những công thức cơ bản để giải bài tập cực trị của hàm trùng phương trong chuyên đề hàm số lớp 12, còn tồn tại những công thức giải một số trong những dạng phức tạp, khó. Với 3 điểm cực trị trên đồ thị hàm số hàm trùng phương lần lượt là A, B, C. Ta có  Với Đk ab < 0 thì: + Tam giác vuông ABC cân tại a khi : b³+8a=0 + Tam giác ABC đều khi: b³+24a=0 + Tam giác ABC có trọng tâm O: b²= 6ac + Tam giác ABC có trực tâm O: b² +8a -4ac = 0 + Tam giác ABC có O là tâm đường tròn nội tiếp: b³ – 8a – 4abc = 0 + Tam giác ABC có O là tâm đường tròn ngoại tiếp: b³ – 8a – 8abc = 0 + Tam giác ABC có nửa đường kính đường tròn ngoại tiếp là R:  + Tam giác ABC có nửa đường kính đường tròn nội tiếp r:  + Tam giác ABC có diện tính S: 32a³S²+b5 = 0 + Đồ thị hàm số (C): y = x4 + bx2 + c cắt trục hoành tại 4 điểm phân biệt tạo thành cấp số cộng: b² = 100/9.ac Trên đấy là tổng hợp toàn bộ những công thức tính nhanh bài tập về cực trị của hàm số lớp 12. Hy vọng với số công thức này, từ giờ teen 2K1 sẽ thuận tiện và đơn thuần và giản dị giải được những bài tập về cực trị hàm số. Các em trọn vẹn có thể vận dụng chính những công thức trên để “cày 172 bài tập cực trị của hàm số lớp 12 từ dễ đến khó” Trọn bộ công thức, phương pháp giải nhanh mọi dạng toán thi THPT Quốc gia Sách luyện thi THTP Quốc gia môn Toán thứ nhất tổng hợp kiến thức và kỹ năng cả 3 năm Trong chuyên đề đồ thị hàm số lớp 12 còn thật nhiều dạng bài tập khác thường xuất hiện trong đề thi như: Tìm GTLN GTNN của hàm số lớp 12, xét tính đơn điệu của hàm số… Mà chuyên đề đồ thị hàm số chỉ là một chuyên đề nhỏ trong thật nhiều chuyên đề Toán những em cần ôn luyện để thi THPT Quốc gia. Với bất kể phần kiến thức và kỹ năng nào, những em đều phải có phương pháp, công thức giải nhanh. Để giúp việc học Toán của những em “nhẹ tựa lông hồng”, CCBook xin trình làng sách Đột phá 8+ kì thi THTP Quốc gia môn Toán. Sách thứ nhất khối mạng lưới hệ thống kiến thức và kỹ năng 3 nămNắm được Xu thế ra đề thi kiểm tra tổng hợp kiến thức và kỹ năng 3 năm. CCBook đã cho trình làng sách luyện thi THPT Quốc gia môn Toán mang tên Đột phá 8+. Cuốn sách thứ nhất tổng hợp kiến thức và kỹ năng trọng tâm của tất cả 3 năm học. Kiến thức lớp 10, 11 được trình diễn cô đọng, dễ hiểu dễ nhớ. Kiến thức lớp 12 được trình diễn theo từng bài bám sát nội dung SGK. Đặc biệt là phần trình diễn lý thuyết và ví dụ tuy nhiên tuy nhiên. Học sinh trọn vẹn có thể đọc đến đâu hiểu đến đó. Tổng hợp những phương pháp, công thức giải nhanh cho mọi dạng bài tậpSách luyện thi THPT Quốc gia của CCBook sẽ tương hỗ những em nắm được toàn bộ công thức giải nhanh từng dạng bài tập. Các dạng bài từ cơ bản đến nâng cao, thường xuất hiện trong đề thi trong năm. Phần hướng dẫn giải rất rõ ràng để học viên hiểu sâu, nhớ lâu được cách làm bài. Tích hợp nhiều tiện ích học thông minh giúp học viên tăng cấp cải tiến vượt bậc điểm số trong thời hạn ngắnĐiểm số của những em đang lẹt đẹt ở tại mức trung bình? Chỉ còn vài tháng nữa làm thế nào tăng tốc lên mức 7-8 và thậm chí còn là một 9-10? Đột phá 8+ kì thi THPT Quốc gia môn Toán sẽ tương hỗ những em biến điều này thành hiện thực. Ngoài nội dung chất lượng, sách còn tích hợp thêm những tiện ích học thông minh như: – Hệ thống thi thử trực tuyến CCTest. – Hệ thống video bài giảng. – Group giải đáp học tập trên Facebook. Các em sẽ tiến hành trao toàn bộ những tiện ích trên khi sở hữu cuốn sách “chất hơn nước cất” này. Để sở hữu ngay bản đọc thử của cuốn sách hãy comment ngay phía dưới. CCBook sẽ phản hồi trong thời hạn sớm nhất. Bài viết này, boxthuthuat sẽ hướng dẫn những bạn lý thuyết về cực trị của hàm số, cùng cách tìm cực trị cũng như những dạng bài tập về tìm giá trị cực lớn, cực tiểu của hàm số.  Khái niệm cực trị hàm sốGiả sử hàm số f xác lập trên tập hợp D (D ⊂ ℝ) và xo∈ D a) xo được gọi là một điểm cực lớn của hàm số f nếu tồn tại một khoảng chừng (a; b) chứa điểm xo sao cho:  Khi đó f(xo) được gọi là giá trị cực lớn của hàm số f . b) xo được gọi là một điểm cực tiểu của hàm số f nếu tồn tại một khoảng chừng (a; b) chứa điểm xo sao cho:  Khi đó f(xo) được gọi là giá trị cực tiểu của hàm số f . Giá trị cực lớn và giá trị cực tiểu được gọi chung là cực trị Nếu xo là một điểm cực trị của hàm số f thì người ta nói rằng hàm số f đạt cực trị tại điểm xo . Như vậy: Điểm cực trị phải là một điểm trong của tập hợp D (D ⊂ ℝ) Nhấn mạnh: xo ∈ (a; b) ⊂ D nghĩa là xo là một điểm trong của D  Chú ý
Điều kiện cần để hàm số đạt cực trịĐịnh lý 1: Giả sử hàm số f đạt cực trị tại điểm xo. Khi đó , nếu f có đạo hàm tại điểm xo thì f ‘(xo) = 0 Chú ý:
Ví dụ : Hàm số y = |x| và hàm số y = x3 Điều kiện đủ để hàm số đạt cực trịĐịnh lý 2: Giả sử hàm số f liên tục trên khoảng chừng (a; b) chứa điểm xo và có đạo hàm trên những khoảng chừng (a; xo) và (xo; b). Khi đó:   Định lý 3: Giả sử hàm số f có đạo hàm cấp một trên khoảng chừng (a; b) chứa điểm xo ; f ‘(xo) = 0 và f có đạo hàm cấp hai khác 0 tại điểm xo a) Nếu f ”(xo) < 0 thì hàm số f đạt cực lớn tại điểm xo Chú ý: Không cần xét hàm số f có hay là không tồn tại đạo hàm tại điểm x = xo nhưng không thể bỏ qua Đk hàm số liên tục tại điểm xo  Bài tập tìm cực trị của hàm sốDạng 1: Tìm những điểm cực trị của hàm sốQuy tắc 1: Áp dụng định lý 2
Quy tắc 2: Áp dụng định lý 3
– Nếu f ”(xi) < 0 thì hàm số đạt cực lớn tại điểm xi – Nếu f ”(xi) > 0 thì hàm số đạt cực tiểu tại điểm xi          Dạng 2: Tìm Đk để hàm số có cực trịPhương pháp: Sử dụng định lí 2 và định lí 3 Chú ý * Hàm số f (xác lập trên D) có cực trị ⇔ ∃ xo ∈ D thỏa mãn thị hiếu hai Đk sau:
* Nếu f ‘(x) là một tam thức bậc hai hoặc triệt tiêu và cùng dấu với một tam thức bậc hai thì hàm có cực trị ⇔ phương trình f ‘(x) có hai nghiệm phân biệt thuộc tập xác lập.           Dạng 3: Tìm Đk để những điểm cực trị của hàm số thỏa mãn thị hiếu Đk cho trướcPhương pháp:
Chú ý:
      Dạng 4 : Ứng dụng cực trị của hàm số trong bài toán đại số  Trên đấy là san sẻ về cực trị của hàm số, cùng những bài tập tìm giá trị cực tiểu, giá trị cực lớn của hàm số. Hi vọng qua những san sẻ này, những bạn sẽ trọn vẹn có thể thuận tiện và đơn thuần và giản dị xử lý và xử lý những bài tập dạng này. |
Video Phương pháp giải cực trị hàm số ?
Một số hướng dẫn một cách rõ ràng hơn về đoạn Clip Phương pháp giải cực trị hàm số tiên tiến và phát triển nhất .
Share Link Cập nhật Phương pháp giải cực trị hàm số miễn phí
Bạn đang tìm một số trong những Share Link Down Phương pháp giải cực trị hàm số Free.
#Phương #pháp #giải #cực #trị #hàm #số
