Bí kíp Hướng dẫn Cho hình chóp sabc có đáy là tam giác đều, mặt bên SAB là tam giác vuông cân tại S Chi Tiết
Bạn đang tìm kiếm từ khóa Cho hình chóp sabc có đáy là tam giác đều, mặt bên SAB là tam giác vuông cân tại S 2022-07-14 16:49:55 san sẻ Mẹo về trong nội dung bài viết một cách Mới Nhất.
Phương pháp giải: – Tìm tâm mặt cầu ngoại tiếp hình chóp (S.ABC) – Tính nửa đường kính (R) của mặt cầu ngoại tiếp đó. – Diện tích của mặt cầu ngoại tiếp hình chóp được xem bởi công thức (S = 4pi R^2) Lời giải rõ ràng: 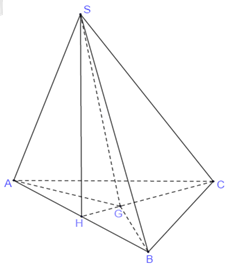 Gọi (H) là trung điểm của (AB), (G) là trọng tâm tam giác (ABC). Tam giác (SAB) vuông cân tại (S) nên (SH bot left( ABC right)) Mặt khác (SAB) nằm trong mặt phẳng vuông góc với đáy nên (SH bot left( ABC right)) Tam giác (ABC) đều nên (G) là trọng tâm tam giác thì (GA = GB = GC) (AB = a Rightarrow CH = dfracsqrt 3 2a Rightarrow left{ beginarraylGH = dfrac13CH = dfracsqrt 3 6a\CG = dfrac23CH = dfracsqrt 3 3aendarray right.) Tam giác (SAB) vuông cân tại (S) nên (SH = dfrac12AB = dfraca2) (SH bot left( ABC right) Rightarrow SH bot HG Rightarrow SG = sqrt SH^2 + HG^2 = sqrt left( dfrac12a right)^2 + left( dfracsqrt 3 6a right)^2 = dfracsqrt 3 3a) Suy ra (GS = GA = GB = GC = dfracsqrt 3 3a), do vậy (G) là tâm mặt cầu ngoại tiếp khối chóp và (R = dfracsqrt 3 3a) Diện tích của mặt cầu ngoại tiếp khối chóp là (S = 4pi R^2 = 4pi left( dfracsqrt 3 3a right)^2 = dfrac4pi a^23). Chọn B. Giải rõ ràng: 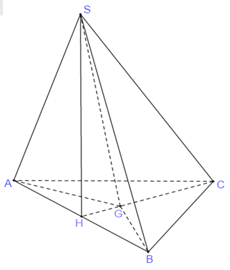 Gọi (H) là trung điểm của (AB), (G) là trọng tâm tam giác (ABC). Tam giác (SAB) vuông cân tại (S) nên (SH bot left( ABC right)) Mặt khác (SAB) nằm trong mặt phẳng vuông góc với đáy nên (SH bot left( ABC right)) Tam giác (ABC) đều nên (G) là trọng tâm tam giác thì (GA = GB = GC) (AB = a Rightarrow CH = dfracsqrt 3 2a Rightarrow left{ beginarraylGH = dfrac13CH = dfracsqrt 3 6a\CG = dfrac23CH = dfracsqrt 3 3aendarray right.) Tam giác (SAB) vuông cân tại (S) nên (SH = dfrac12AB = dfraca2) (SH bot left( ABC right) Rightarrow SH bot HG Rightarrow SG = sqrt SH^2 + HG^2 = sqrt left( dfrac12a right)^2 + left( dfracsqrt 3 6a right)^2 = dfracsqrt 3 3a) Suy ra (GS = GA = GB = GC = dfracsqrt 3 3a), do vậy (G) là tâm mặt cầu ngoại tiếp khối chóp và (R = dfracsqrt 3 3a) Diện tích của mặt cầu ngoại tiếp khối chóp là (S = 4pi R^2 = 4pi left( dfracsqrt 3 3a right)^2 = dfrac4pi a^23). Chọn B. Cho hình chóp. $S.ABC$ có đáy là tam giác đều, mặt bên $SAB$ là tam giác vuông cân tại $S$ và nằm trong mặt?Cho hình chóp. (S.ABC) có đáy là tam giác đều, mặt bên (SAB) là tam giác vuông cân tại (S) và nằm trong mặt phẳng vuông góc với đáy. Biết (SA=asqrt2), tính góc giữa (SC) và mặt phẳng ((SAB)). A. (30^circ ). B. (60^circ ). C. (90^circ ). D. (45^circ ). đã hỏi trong Lớp 12 Toán học · 01:11 01/04/2021 Cho hình chóp S.ABC có đáy là tam giác đều, mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy, biết SA=a2, tính góc giữa SC và (SAB) A. 30°B. 60°C. 90°D. 45° Câu hỏi hot cùng chủ đề
LIVESTREAM 2K4 ÔN THI THPT QUỐC GIA 2022
UNIT 9: LANGUAGE – NGỮ PHÁP TRỌNG TÂM BUỔI 2 – 2k5 Livestream TIẾNG ANH cô QUỲNH TRANG Tiếng Anh (mới) Xem thêm … |
đoạn Clip Cho hình chóp sabc có đáy là tam giác đều, mặt bên SAB là tam giác vuông cân tại S ?
Một số hướng dẫn một cách rõ ràng hơn về Review Cho hình chóp sabc có đáy là tam giác đều, mặt bên SAB là tam giác vuông cân tại S tiên tiến và phát triển nhất .
Share Link Cập nhật Cho hình chóp sabc có đáy là tam giác đều, mặt bên SAB là tam giác vuông cân tại S miễn phí
Bạn đang tìm một số trong những ShareLink Download Cho hình chóp sabc có đáy là tam giác đều, mặt bên SAB là tam giác vuông cân tại S Free.
#Cho #hình #chóp #sabc #có #đáy #là #tam #giác #đều #mặt #bên #SAB #là #tam #giác #vuông #cân #tại