Bí kíp về Bài 52 SBT Toán 9 Tập 2 trang 61 Mới Nhất
Heros đang tìm kiếm từ khóa Bài 52 SBT Toán 9 Tập 2 trang 61 2022-10-17 04:30:53 san sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách 2021.
 Bài 52 trang 61 Sách bài tập Toán 9 Tập 2: Trong một phòng họp có 360 ghế được xếp thành những dãy và số ghế trong những dãy đều bằng nhau. Xem rõ ràng »  Bài 51, 52, 53, 54, 55, 56, 57, 58, 59 trang 61 SBT Toán 9 Tập 2 | Giải sách bài tập Toán lớp 9 hay và rõ ràng nhất – Các bài giải bài tập sách bài tập … Xem rõ ràng »  25 thg 10, 2019 · Bài 51 trang 61 SBT toán 9 tập 2. Giải bài 51 trang 61 sách bài tập toán 9. Cho một số trong những có hai chữ số. Tổng hai chữ số của chúng bằng 10. Xem rõ ràng »  Câu 51 trang 61 Sách bài tập (SBT) Toán 9 tập 2. Cho một số trong những có hai chữ số. Tổng hai chữ số của chúng bằng 10. Tích hai chữ số ấy nhỏ hơn số đã cho là 12. Xem rõ ràng »  Giải bài tập trang 61 bài 8 Giải bài toán bằng phương pháp lập phương trình Sách bài tập (SBT) Toán 9 tập 2. Câu 55: Người ta trộn 8g chất lỏng này với 6g chất … Xem rõ ràng »  Xếp hạng 5,0 (1) Giải SBT Toán 9 trang 61, 62 Tập 2: Bài 8: Giải bài toán bằng phương pháp lập phương trình, tương hỗ những em học viên củng cố kiến thức và kỹ năng và làm rõ phương pháp giải … Xem rõ ràng »  4 thg 5, 2022 · Giải vướng mắc 3 Trang 61 SGK toán lớp 9 – Tập 2, phần vướng mắc lý thuyết bài Ôn tập chương 4: Hàm số y = ax² (a ≠ 0) – Phương trình bậc hai … Xem rõ ràng »  Câu 59 trang 61 Sách bài tập (SBT) Toán 9 tập 2. Tính vận tốc của xuồng. – sachbaitap.com. Xem rõ ràng »  Xếp hạng 5,0 (1) Mẹo giải bài tập 4 trang 61 sgk đại số lớp 9 tập 2 ôn tập chương IV phần vướng mắc. Nêu cách tìm hai số, biết tổng S và tích P của chúng. Xem rõ ràng »  Xếp hạng 5,0 (1) Hướng dẫn làm bài tập 5 trang 61 sgk đại số lớp 9 tập 2 ôn tập chương IV phần vướng mắc. Nêu cách giải phương trình trùng phương ax4+bx2+c=0 (a ≠ 0). Xem rõ ràng »  Ôn tập chương 2 Toán 9 tập 1: giải bài 32, 33, 34, 35, 36, 37 trang 61; Giải bài 38 SGK trang 62: Ôn tập chương 2 Đại số Toán lớp 9 tập 1: Hàm. Xem rõ ràng »  01 Đề bài: Bài 51: trang 61 sbt Toán 9 tập 2. Cho một số trong những có hai chữ số. Tổng hai chữ số của chúng bằng 10. Tích hai chữ số ấy nhỏ hơn số đã cho là 12. Xem rõ ràng »  Câu 51 trang 61 Sách bài tập (SBT) Toán 9 tập 2 – Bài 8: Giải bài toán bằng … Gọi chữ số hàng trăm là x; Đk: x ∈ N*; x≤ 9 thì chữ số hàng cty chức năng … Xem rõ ràng »  Bài 52 trang 61 SBT toán 9 tập 2. Đề bài. Trong một phòng họp có ghế được xếp thành những dãy và số ghế trong những dãy đều bằng nhau. Xem rõ ràng » Câu 51 trang 61 Sách bài tập (SBT) Toán 9 tập 2 Cho một số trong những có hai chữ số. Tổng hai chữ số của chúng bằng 10. Tích hai chữ số ấy nhỏ hơn số đã cho là 12. Tìm số đã cho. Giải Gọi chữ số hàng trăm là x; Đk: x ∈ N*; x≤ 9 thì chữ số hàng cty chức năng là 10 – x Giá trị của số đó bằng: 10x + 10 –x =9x +10 Tích của hai chữ số nhỏ hơn số đã cho là 12, ta có phương trình: (eqalign& xleft( 10 – x right) = 9x + 10 – 12 cr & Leftrightarrow 10x – x^2 = 9x – 2 cr & Leftrightarrow x^2 – x – 2 = 0 cr ) Phương trình có dạng: (a – b + c = 0) (eqalign& 1 – left( – 1 right) + left( – 2 right) = 1 + 1 – 2 = 0 cr & x_1 = – 1;x_2 = – – 2 over 1 = 2 cr ) Vì x ∈ N* nên x1 = -1 không thỏa mãn thị hiếu Đk bài toán: loại Vậy chữ số hàng trăm là 2, chữ số hàng cty chức năng: 10 – 2 = 8 Số cần tìm 28. Câu 52 trang 61 Sách bài tập (SBT) Toán 9 tập 2 Trong một phòng họp có 360 ghế được xếp thành những dãy và số ghế trong những dãy đều bằng nhau. Có một lần phòng họp phải xếp thêm một dãy ghế và mỗi dãy tăng 1 ghế (số ghế trong những dãy vẫn bằng nhau) để sở hữu đủ chỗ cho 400 đại biểu. Hỏi thường thì trong phòng có bao nhiêu dãy ghế? Giải Gọi số dãy ghế ban sơ của phòng họp là x (dãy); Đk: x ∈ N* Thì số ghế ngồi trong một dãy là (360 over x) (ghế) Số dãy ghế sau khoản thời hạn tăng thêm là (x + 1) (dãy) Số ghế trong một dãy sau khoản thời hạn tăng là (400 over x + 1) (ghế) Theo bài ra ta có phương trình: (400 over x + 1 – 360 over x = 1) (eqalign& Leftrightarrow 400x – 360left( x + 1 right) = xleft( x + 1 right) cr & Leftrightarrow 400x – 360x – 360 = x^2 + x cr & Leftrightarrow x^2 – 39x + 360 = 0 cr & Delta = 1521 – 1440 = 81 > 0 cr & sqrt Delta = sqrt 81 = 9 cr & x_1 = 39 + 9 over 2.1 = 48 over 2 = 24 cr & x_2 = 39 – 9 over 2.1 = 30 over 2 = 15 cr ) Cả hai giá trị đều thỏa mãn thị hiếu Đk bài toán Vậy số dãy ghế ban sơ là 24 dãy hoặc 15 dãy. Câu 53 trang 61 Sách bài tập (SBT) Toán 9 tập 2 Một công ty vận tải lối đi bộ dự tính dùng loại xe lớn để chở 15 tấn rau theo một hợp đồng. Nhưng khi vào việc, công ty không hề xe lớn nên phải thay bằng những xe có trọng tải nhỏ hơn nửa tấn. Để đảm bảo thời hạn đã hợp đồng, công ti phải dùng một số trong những lượng xe nhiều hơn thế nữa số xe dự tính là một trong những xe). Hỏi trọng tải của mỗi xe nhỏ là bao nhiêu tấn? Giải Gọi trọng tải của xe nhỏ là x (tấn); Đk: x > 0 Thì trọng tải của xe lớn là (x + 0,5) (tấn) Số lượng xe lớn dự tính để chở là: (15 over x + 0,5) (xe) Số lượng xe nhỏ chở hết 15 tấn là: (15 over x) (xe) Ta có phương trình: (15 over x – 15 over x + 0,5 = 1) (eqalign& Leftrightarrow 15left( x + 0,5 right) – 15x = xleft( x + 0,5 right) cr & Leftrightarrow 15x + 7,5 – 15x = x^2 + 0,5x cr & Leftrightarrow x^2 + 0,5x – 7,5 = 0 cr & Delta = 1^2 – 4.2.left( – 15 right) = 1 + 120 = 121 > 0 cr & sqrt Delta = sqrt 121 = 11 cr & x_1 = – 1 + 11 over 2.2 = 10 over 4 = 2,5 cr & x_2 = – 1 – 11 over 2.2 = – 12 over 4 = – 3 cr ) x2 = -3 < 0 không thỏa mãn thị hiếu Đk bài toán: loại Vậy trọng tải của một xe nhỏ là 2,5 tấn Câu 54 trang 61 Sách bài tập (SBT) Toán 9 tập 2 Một tổ máy trộn bê tông phải sản xuất 450m3 bê tông cho một đập thủy lợi trong thuở nào hạn quy định. Nhờ tăng năng suất mỗi ngày 4,5m3 nên 4 ngày trước thời hạn quy định tổ đã sản xuất được 96% việc làm). Hỏi thời hạn quy định là bao nhiêu ngày? Giải Gọi thời hạn quy định trong việc làm là x (ngày); Đk: x > 4 Năng suất quy định là: (450 over x(m^3)) 4 ngày trước thời hạn quy định tổ mãy sản xuất được là: (450.96 over 100 = 432(m^3)) Năng suất thực tiễn làm là: (432 over x – 4(m^3)) Ta có phương trình: (eqalign& 432 over x – 4 – 450 over x = 4,5 cr & Leftrightarrow 432x – 450left( x – 4 right) = 4,5xleft( x – 4 right) cr & Leftrightarrow 432x – 450x + 1800 = 4,5x^2 – 18x cr & Leftrightarrow 4,5x^2 – 1800 = 0 cr & Leftrightarrow x^2 – 400 = 0 cr & Leftrightarrow x^2 = 400 cr & Rightarrow x_1 = 20;x_2 = – 20 cr ) Giá trị: x2 = -20 < 4 không thỏa mãn thị hiếu Đk bài toán: loại Vậy thời hạn quy định là 20 ngày. Giaibaitap.me Page 2Câu 55 trang 61 Sách bài tập (SBT) Toán 9 tập 2 Người ta trộn 8g chất lỏng này với 6g chất lỏng khác có khối lượng riêng nhỏ hơn là 0,2g/cm3 để được một hỗn hợp có khối lương riêng là 0,7g/cm3. Tìm khối lượng riêng của mỗi chất lỏng. Giải Gọi khối lượng riêng của chất lỏng thứ hai là x (g/cm3); Đk: x > 0 Thì khối lượng riêng của chất lỏng thứ nhất là (x + 0,2) (g/cm3) Thể tích của chất lỏng thứ nhất là: (8 over x + 0,2) (g/cm3) Thể tích của chất lỏng thứ hai là: (6 over x(cm^3)) Thể tích của hỗn hợp là: (8 + 6 over 0,7 = 14 over 0,7 = 20(cm^3)) Ta có phương trình: (eqalign& 8 over x + 0,2 + 6 over x = 20 cr & Leftrightarrow 8x + 6left( x + 0,2 right) = 20xleft( x + 0,2 right) cr & Leftrightarrow 8x + 6x + 1,2 = 20x^2 + 4x cr & Leftrightarrow 20x^2 – 10x – 1,2 = 0 cr & Delta ‘ = left( – 5 right)^2 – 10.left( – 1,2 right) = 25 + 24 = 49 > 0 cr & sqrt Delta ‘ = sqrt 49 = 7 cr & x_1 = 5 + 7 over 20 = 12 over 20 = 0,6 cr & x_2 = 5 – 7 over 20 = – 0,1 cr ) x2 = -0,1 < 0 không thỏa mãn thị hiếu Đk bài toán: loại Vậy khối lượng riêng của chất lỏng thứ hai là 0,6 (g/cm3) Khối lượng riêng của chất lỏng thứ nhất là 0,6 + 0,2 = 0,8 (g/cm3) Câu 56 trang 61 Sách bài tập (SBT) Toán 9 tập 2 Quãng đường Thanh Hóa – Tp Hà Nội Thủ Đô dài 150km. Một xe hơi từ Tp Hà Nội Thủ Đô vào Thanh Hóa, nghỉ tại Thanh Hóa 3 giờ 15 phút, rồi trở về Tp Hà Nội Thủ Đô, hết toàn bộ 10 giờ. Tính vận tốc của xe hơi lúc về, biết rằng vận tốc lúc đi to nhiều hơn vận tốc lúc về là 10km/h. Giải Gọi vận tốc lúc về là x (km/h); Đk: x > 0 Thì vận tốc lúc đi là: (x + 10) (km/h) Thời gian lúc đi là: (150 over x + 10) (giờ) Thời gian lúc về là: (150 over x) (giờ) Ta có phương trình: (eqalign& 150 over x + 10 + 31 over 4 + 150 over x = 10 cr & Leftrightarrow 150 over x + 10 + 150 over x = 10 – 13 over 4 cr & Leftrightarrow 150 over x + 10 + 150 over x = 27 over 4 cr & Leftrightarrow 600x + 600left( x + 10 right) = 27xleft( x + 10 right) cr & Leftrightarrow 600x + 600x + 6000 = 27x^2 + 270x cr & Leftrightarrow 27x^2 – 930x – 6000 = 0 cr & Leftrightarrow 9x^2 – 310x – 2000 = 0 cr & Delta ‘ = 24025 + 18000 = 42025 > 0 cr & sqrt Delta ‘ = sqrt 42025 = 205 cr & x_1 = 155 + 205 over 9 = 40 cr & x_2 = 155 – 205 over 9 = – 50 over 9 cr ) (x_2 = – 50 over 9 < 0) không thỏa mãn thị hiếu Đk: loại Vận tốc xe hơi lúc về là 40 km/h Câu 57 trang 61 Sách bài tập (SBT) Toán 9 tập 2 Hai trường bay Tp Hà Nội Thủ Đô và Tp Thành Phố Đà Nẵng cách nhau 600km. Một máy bay cánh quạt từ Tp Thành Phố Đà Nẵng đi Tp Hà Nội Thủ Đô. Sau đó 10 phút một máy bay phản lực từ Tp Hà Nội Thủ Đô bay đi Tp Thành Phố Đà Nẵng với vận tốc to nhiều hơn vận tốc của máy bay cánh quạt là 300km/h. Nó đến Tp Thành Phố Đà Nẵng trước lúc máy bay kia đến Tp Hà Nội Thủ Đô 10 phút. Tính vận tốc của mỗi máy bay. Giải Gọi vận tốc của máy bay cánh quạt là x (km/h); Đk: x > 0 Thì vận tốc của máy bay phản lực là (left( x + 300 right)) (km/h) Thời gian máy bay cánh quạt bay là: (600 over x) (giờ) Thời gian máy bay phản lực bay là: (600 over x + 300) (giờ) Máy bay phản lực bay sau 10 phút và đến trước 10 phút nên thời hạn máy bay phản lực bay thấp hơn máy bay cánh quạt là: 10 phút + 10 phút = 20 phút = (1 over 3) giờ Ta có phương trình: (eqalign& 600 over x – 600 over x + 300 = 1 over 3 cr & Rightarrow 3.600left( x + 300 right) – 3.600x = xleft( x + 300 right) cr & Leftrightarrow 1800x + 540000 – 1800x = x^2 + 300x cr & Leftrightarrow x^2 + 300x – 540000 = 0 cr & Delta ‘ = 22500 + 540000 = 562500 > 0 cr & sqrt Delta ‘ = sqrt 562500 = 750 cr & x_1 = – 150 + 750 over 1 = 600 cr & x_2 = – 150 – 750 over 1 = – 900 cr ) x2 = -900 < 0 không thỏa mãn thị hiếu Đk: loại Vậy: vận tốc máy bay cánh quạt là 600 km/h Vận tốc của máy bay phản lực là 600 + 300 = 900 km/h Câu 58 trang 61 Sách bài tập (SBT) Toán 9 tập 2 Tp Hà Nội Thủ Đô cách Tỉnh Nam Định 90km. Hai xe hơi khởi hành đồng thời, xe thứ nhất từ Tp Hà Nội Thủ Đô, xe thứ hai từ Tỉnh Nam Định và đi ngược chiều nhau. Sau 1 giờ chúng gặp nhau. Tiếp tục đi, xe thứ hai tới Tp Hà Nội Thủ Đô trước lúc xe thứ nhất tới Tỉnh Nam Định là 27 phút. Tính vận tốc mỗi xe. Giải Gọi vận tốc xe thứ nhất là x (km/h); Đk: 0< x < 90 Vì sau 1 giờ hai xe gặp nhau, vậy quãng đường hai xe đi được trong một giờ là 90 km tức tổng vận tốc của hai xe là 90km/h nên vận tốc của xe thứ hai đi là 90 – x (km/h) Quãng đường xe thứ nhất tiếp tục đi là: 90 – x (km) Thời gian xe thứ nhất đi phần đường còn sót lại là (90 – x over x) giờ Quãng đường xe thứ hai tiếp tục đi là x (km) Thời gian xe thứ hai đi đoạn còn sót lại là (x over 90 – x) giờ Xe thứ hai đến Tp Hà Nội Thủ Đô trước xe thứ nhất đến Tỉnh Nam Định là 27 phút bằng (9 over 20) giờ. Ta có phương trình: (eqalign& 90 – x over x – x over 90 – x = 9 over 20 cr & Rightarrow 20left( 90 – x right)^2 – 20x^2 = 9xleft( 90 – x right) cr & Leftrightarrow 20left( 8100 – 180x + x^2 right) – 20x^2 = 810x – 9x^2 cr & Leftrightarrow 162000 – 3600x + 20x^2 – 20x^2 – 810x + 9x^2 = 0 cr & Leftrightarrow 9x^2 – 4410x + 162000 = 0 cr & Leftrightarrow x^2 – 490x + 1800 = 0 cr & Delta ‘ = 60025 – 18000 = 42025 > 0 cr & sqrt Delta ‘ = sqrt 42025 = 205 cr & x_1 = 245 + 205 over 1 = 450 cr & x_2 = 245 – 205 over 1 = 40 cr ) x2 = 450 > 90 không thỏa mãn thị hiếu Đk: loại. Vậy: vận tốc xe thứ nhất là 40km/h Vận tốc xe thứ hai là (90 – 40 = 50) km/h Giaibaitap.me Page 3Câu 59 trang 61 Sách bài tập (SBT) Toán 9 tập 2 Một xuồng máy xuôi dòng 30km và ngược dòng 28km hết thuở nào hạn bằng thời hạn mà xuồng đi 59,5 km trên mặt hồ yên lặng. Tính vận tốc của xuồng khi đi trên hồ biết rằng vận tốc của nước chảy trong sông là 3km/h. Giải Gọi vận tốc thuyền khi đi trên hồ là x (km/h); Đk: x > 3 Vận tốc khi đi xuôi dòng trên sông là x + 3 (km/h) Vận tốc khi đi ngược dòng trên sông là x – 3 (km/h) Thời gian đi xuôi dòng bằng (30 over x + 3) giờ Thời gian đi ngược dòng bằng (28 over x – 3) giờ Thời gian đi trên hồ bằng (59,5 over x) giờ Ta có phương trình: (eqalign& 30 over x + 3 + 28 over x – 3 = 59,5 over x cr & Rightarrow 60xleft( x – 3 right) + 56xleft( x + 3 right) = 119left( x + 3 right)left( x – 3 right) cr & Leftrightarrow 60x^2 – 180x + 56x^2 + 168x = 119x^2 – 1071 cr & Leftrightarrow 3x^2 + 12x – 1071 = 0 cr & Leftrightarrow x^2 + 4x – 357 = 0 cr & Delta ‘ = 4 + 357 = 361 > 0 cr & sqrt Delta ‘ = sqrt 361 = 19 cr & x_1 = – 2 + 19 over 1 = 17 cr & x_2 = – 2 – 19 over 1 = – 21 cr ) x2 = -21 < 3 không thỏa mãn thị hiếu Đk: loại. Vậy vận tốc thuyền đi trên hồ yên lặng là 17km/h Câu 60 trang 62 Sách bài tập (SBT) Toán 9 tập 2 Một bè gỗ được thả trôi trên sông từ đập Ya-ly. Sau khi thả bè gỗ 5 giờ 20 phút, một xuồng máy cũng xuất phát từ đập Ya-ly đuổi theo và đi được 20km thì gặp bè. Tính vận tốc của bè biết rằng xuồng máy chạy nhanh hơn bè 12km/h. Giải Gọi vận tốc của bè là x (km/h); Đk: x > 0 Thì vận tốc của ca nô là x + 12 km/h Thời gian bè từ lúc trôi đến lúc gặp ca nô là (20 over x) giờ Thời gian ca nô lúc đi đến lúc gặp bè là (20 over x + 12) giờ Bè gỗ trôi trước ca nô 5 giờ 20 phút bằng (51 over 3) giờ = (16 over 3) giờ Ta có phương trình: (eqalign& 20 over x – 20 over x + 12 = 16 over 3 cr & Rightarrow 60left( x + 12 right) – 60x = 16xleft( x + 12 right) cr & Leftrightarrow 60x + 720 – 60x = 16x^2 + 192x cr & Leftrightarrow 16x^2 + 192x – 720 = 0 cr & Leftrightarrow x^2 + 12x – 45 = 0 cr & Delta ‘ = 6^2 – 1left( – 45 right) = 36 + 45 = 81 > 0 cr & sqrt Delta ‘ = sqrt 81 = 9 cr & x_1 = – 6 + 9 over 1 = 3 cr & x_2 = – 6 – 9 over 1 = – 15 cr ) x2 = -15 < 0 không thỏa mãn thị hiếu Đk: loại. Vậy vận tốc của bè gỗ trôi là 3km/h Câu 61 trang 62 Sách bài tập (SBT) Toán 9 tập 2 Nếu mở cả hai vòi nước chảy vào một trong những bể cạn thì sau 2 tiếng 55 phút bể đầy nước) Nếu mở riêng từng vòi thì vòi thứ nhất làm đầy bể nhanh hơn vòi thứ hai là 2 tiếng. Hỏi nếu mở riêng từng vòi thì mỗi vòi chảy bao lâu đầy bể? Giải Gọi thời hạn chảy riêng đầy bể của vòi thứ nhất là x giờ Điều kiện: (x > 211 over 12) Thì thời hạn chảy riêng đầy bể của vòi thứ hai là x + 2 tiếng Trong một giờ vòi thứ nhất chảy được (1 over x) bể Trong một giờ vòi thứ hai chảy được (1 over x + 2) bể Trong một giờ cả hai vòi chảy được (1:211 over 12 = 12 over 35) bể Ta có phương trình: (eqalign& 1 over x + 1 over x + 2 = 12 over 35 cr & Rightarrow 35left( x + 2 right) + 35x = 12xleft( x + 2 right) cr & Leftrightarrow 35x + 70 + 35x = 12x^2 + 24x cr & Leftrightarrow 12x^2 – 46x – 70 = 0 cr & Leftrightarrow 6x^2 – 23x – 35 = 0 cr & Delta = 529 + 840 = 1369 > 0 cr & sqrt Delta = sqrt 1369 = 37 cr & x_1 = 23 + 37 over 2.6 = 5 cr & x_2 = 23 – 37 over 2.6 = – 7 over 6 cr ) x2 = ( – 7 over 6 < 211 over 12) không thỏa mãn thị hiếu Đk: loại. Vậy: vòi thứ nhất chảy riêng đầy bể sau 5 giờ Vòi thứ hai chảy riêng đầy bể sau 5 + 2 = 7 giờ Câu 62 trang 62 Sách bài tập (SBT) Toán 9 tập 2 Hai đội công nhân cùng làm một quãng đường thì 12 ngày xong việc) Nếu đội thứ nhất làm một mình hết nửa việc làm, rồi đội thứ hai tiếp tục một mình làm nốt phần việc còn sót lại thì hết toàn bộ 25 ngày. Hỏi mỗi đội làm một mình thì bao lâu xong việc? Giải Gọi thời hạn đội thứ nhất làm riêng xong nửa việc làm là x ngày Điều kiện: 6 < x < 25 Thì thời hạn làm riêng xong nửa việc làm của đội thứ hai là 25 – x ngày Trong 1 ngày đội thứ nhất làm được (1 over 2x) việc làm Trong một ngày đội thứ hai làm được (1 over 2left( 25 – x right)) việc làm Trong một ngày cả hai đội làm được (1 over 12) việc làm Ta có phương trình: (eqalign& 1 over 2x + 1 over 2left( 25 – x right) = 1 over 12 cr & Rightarrow 24left( 25 – x right) + 24x = 4xleft( 25 – x right) cr & Leftrightarrow 600 – 24x + 24x = 100x – 4x^2 cr & Leftrightarrow 4x^2 – 100x + 600 = 0 cr & Leftrightarrow x^2 – 25x + 150 = 0 cr & Delta = 625 – 600 = 25 > 0 cr & sqrt Delta = sqrt 25 = 5 cr & x_1 = 25 + 5 over 2.1 = 15 cr & x_2 = 25 – 5 over 2.1 = 10 cr ) Cả hai giá trị thỏa mãn thị hiếu Đk bài toán Vậy đội thứ nhất làm riêng xong việc làm 30 ngày thì đội thứ hai làm riêng xong trong 20 ngày. Hoặc đội thứ nhất làm riêng xong việc làm trong 20 ngày thì đội thứ hai làm riêng xong trong 30 ngày. Giaibaitap.me Page 4Câu 63 trang 62 Sách bài tập (SBT) Toán 9 tập 2 Cho tam giác ABC vuông cân có AB = AC = 12cm. Điểm M chạy trên AB) Tứ giác MNCP là một hình bình hành có đỉnh N thuộc cạnh AC (h.6). Hỏi khi M cách A bao nhiêu thì diện tích quy hoạnh s của hình bình hành bằng 32cm2? 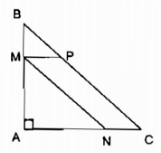 Giải Gọi độ dài đoạn MA = x cm; Đk 0 < x < 12 Vì ∆ ABC vuông cân tại A nên tam giác BMP vuông cân tại M ⇒ MP = MB = AB – AM = 12 – x (cm) Diện tích hình bình hành MNCP bằng MP.MA Suy ra: MP.MA = (12 – x)x Ta có phương trình: (eqalign & left( 12 – x right)x = 32 cr & Rightarrow x^2 – 12x + 32 = 0 cr & Delta ‘ = left( – 6 right)^2 – 1.32 = 36 – 32 = 4 > 0 cr & sqrt Delta ‘ = sqrt 4 = 2 cr & x_1 = 6 + 2 over 1 = 8 cr & x_2 = 6 – 2 over 1 = 4 cr ) Cả hai giá trị x1 = 8 và x2 = 4 thỏa mãn thị hiếu Đk bài toán Vậy điểm M cách điểm A là 8cm hoặc 4cm Câu 64 trang 62 Sách bài tập (SBT) Toán 9 tập 2 Chu vi bánh sau của một máy cày to nhiều hơn chu vi bánh trước là một trong những,5m. Khi đi trên phần đường dài 100m thì bánh trước quay nhiều hơn thế nữa bánh sau 15 vòng. Tính chu vi của mỗi bánh xe. Giải Gọi chu vi của bánh trước là x (m), Đk: x > 0 Chu vi của bánh sau là x + 1,5 (m) Số vòng xoay của bánh trước là (100 over x) vòng Số vòng xoay của bánh sau là (100 over x + 1,5) vòng Ta có phương trình: (eqalign & 100 over x – 100 over x + 1,5 = 15 cr & Rightarrow 100left( x + 1,5 right) – 100x = 15xleft( x + 1,5 right) cr & Leftrightarrow 100x + 150 – 100x = 15x^2 + 22,5x cr & Leftrightarrow 15x^2 + 22,5x – 150 = 0 cr & Leftrightarrow 2x^2 + 3x – 20 = 0 cr & Delta = 3^2 – 4.2.left( – 20 right) = 9 + 160 = 169 > 0 cr & sqrt Delta = sqrt 169 = 13 cr & x_1 = – 3 + 13 over 2.2 = 2,5 cr & x_2 = – 3 – 13 over 2.2 = – 4 cr ) x2 = -4 < 0 không thỏa mãn thị hiếu Đk: loại. Vậy chu vi bánh xe trước bằng 2,5m Chu vi bánh xe sau bằng 2,5 + 1,5 = 4m Câu 65 trang 62 Sách bài tập (SBT) Toán 9 tập 2 Bài toán cổ Ấn Độ Một đàn khỉ phân thành hai nhóm. Nhóm chơi đùa vui vẻ ngoài trời Bằng bình phương một phần tám của đàn. Mười hai con nhảy nhót trên cây. Không khí vui tươi sưởi ấm nơi này. Hỏi có toàn bộ bao nhiêu con khỉ? Giải Gọi số khỉ của đàn là x (con) Điều kiện: x ∈ N* và x ⋮ 8 Nhóm chơi đùa ngoài trời có (left( x over 8 right)^2) con Nhóm nhảy nhót trên cây là 12 con Ta có phương trình: (eqalign & x = left( x over 8 right)^2 + 12 cr & Leftrightarrow x = x^2 over 64 + 12 cr & Leftrightarrow x^2 – 64x + 768 = 0 cr & Delta ‘ = left( – 32 right)^2 – 1.768 = 1024 – 768 = 256 > 0 cr & sqrt Delta ‘ = sqrt 256 = 16 cr & x_1 = 32 + 16 over 1 = 48 cr & x_2 = 32 – 16 over 1 = 16 cr ) Cả hai giá trị x1 = 48 và x2 = 16 thỏa mãn thị hiếu Đk bài toán Vậy đàn khỉ có 48 con hoặc 16 con Câu 66 trang 62 Sách bài tập (SBT) Toán 9 tập 2 Bài toán của Ơ-le Hai nông dân đem 100 quả trứng ra chợ bán. Số trứng của hai người không bằng nhau, nhưng hai người bán tốt số tiền bằng nhau. Một người nói với những người kia: “Nếu số trứng của tôi bằng số trứng của anh thì tôi bán tốt 15 đồng”. Người kia nói: “Nếu số trứng của tôi bằng số trứng của anh thì tôi chỉ bán tốt (62 over 3) đồng thôi”. Hỏi từng người dân có bao nhiêu trứng? Giải Gọi số trứng của người thứ nhất là x (quả) Điều kiện: x ∈ N* và x < 100 Thì số trứng của người thứ hai là 100 – x (quả) Giá tiền một quả trứng của người thứ nhất: (15 over 100 – x) đồng Giá tiền một quả trứng của người thứ hai (20 over 3x) đồng Số tiền người thứ nhất thu được là (15 over 100 – x.x = 15x over 100 – x) đồng Số tiền người thứ hai thu được là: (20 over 3x.left( 100 – x right) = 20left( 100 – x right) over 3x) đồng Ta có phương trình: (eqalign & 15x over 100 – x = 20left( 100 – x right) over 3x cr & Leftrightarrow 45x^2 = 20left( 100 – x right)^2 cr & Leftrightarrow 45x^2 = 20left( 10000 – 200x + x^2 right) cr & Leftrightarrow 45x^2 = 200000 – 4000x + 20x^2 cr & Leftrightarrow 25x^2 + 4000x – 200000 = 0 cr & Leftrightarrow x^2 + 160x – 8000 = 0 cr & Delta ‘ = 80^2 – 1.left( – 8000 right) = 6400 + 8000 = 14400 > 0 cr & sqrt Delta ‘ = sqrt 14400 = 120 cr & x_1 = – 80 + 120 over 1 = 40 cr & x_2 = – 80 – 120 over 1 = – 200 cr ) Giá trị x2 = -200 ∉ N* không thỏa mãn thị hiếu Đk: loại. Vậy: số trứng người thứ nhất là 40 quả Số trứng người thứ hai là 60 quả. Giaibaitap.me Page 5Câu 67 trang 63 Sách bài tập (SBT) Toán 9 tập 2 Cho hai hàm số: (y = 2x – 3) và (y = – x^2) a) Vẽ đồ thị hai hàm số này trong cùng một mặt phẳng tọa độ. b) Tìm tọa độ những giao điểm của hai đồ thị. c) Kiểm nghiệm rằng tọa độ của mỗi giao điểm đều là nghiệm chung của hai phương trình hai ẩn y = 2x – 3 và (y = – x^2) Giải a) Vẽ đồ thị hàm số: (y = 2x – 3) Cho x = 0 ⇒ y = -3(0; -3) Cho y = 0 ⇒ x = 1,5(1,5; 0) Vẽ đồ thị hàm số:
b) Tọa độ giao điểm của hai đồ thị: A(1; -1) và B(-3; -9) c) Thay tọa độ của A và B vào phương trình: (y = 2x – 3) ta có: ( – 1 = 2.1 – 3; – 9 = 2.left( – 3 right) – 3) Thay tọa độ của A và B vào phương trình: (y = – x^2) ( – 1 = – 1^2 = – 1; – 9 = – left( – 3 right)^2 = – 9) Vậy tọa độ của A và B là nghiệm của hệ phương trình: (left{ matrixy = 2x – 3 cr y = – x^2 cr right.) Câu 68 trang 63 Sách bài tập (SBT) Toán 9 tập 2 Giải những phương trình: a) (3x^2 + 4left( x – 1 right) = left( x – 1 right)^2 + 3) b) (x^2 + x + sqrt 3 = sqrt 3 x + 6) c) (x + 2 over 1 – x = 4x^2 – 11x – 2 over left( x + 2 right)left( x – 1 right)) d) (x^2 + 14x over x^3 + 8 = x over x + 2) Giải a) (eqalign& 3x^2 + 4left( x – 1 right) = left( x – 1 right)^2 + 3 cr & Leftrightarrow 3x^2 + 4x – 4 = x^2 – 2x + 1 + 3 cr & Leftrightarrow 2x^2 + 6x – 8 = 0 cr & Leftrightarrow x^2 + 3x – 4 = 0 cr ) Phương trình có dạng: (a + b + c = 0); ta có: (eqalign& 1 + 3 + left( – 4 right) = 0 cr & x_1 = 1;x_2 = – 4 cr ) b) (eqalign& x^2 + x + sqrt 3 = sqrt 3 x + 6 cr & Leftrightarrow x^2 + left( 1 – sqrt 3 right)x + sqrt 3 – 6 = 0 cr & Delta = left( 1 – sqrt 3 right)^2 – 4.1.left( sqrt 3 – 6 right) cr & = 1 – 2sqrt 3 + 3 – 4sqrt 3 + 24 = 28 – 6sqrt 3 cr & = 27 – 2.3sqrt 3 + 1 cr & = left( 3sqrt 3 right)^2 – 2.3sqrt 3 + 1 cr & = left( 3sqrt 3 – 1 right)^2 > 0 cr & sqrt Delta = sqrt left( 3sqrt 3 – 1 right)^2 = 3sqrt 3 – 1 cr & x_1 = sqrt 3 – 1 + 3sqrt 3 – 1 over 2.1 = 4sqrt 3 – 2 over 2 = 2sqrt 3 – 1 cr & x_2 = sqrt 3 – 1 – 3sqrt 3 + 1 over 2.1 = – 2sqrt 3 over 2 = – sqrt 3 cr ) c) (x + 2 over 1 – x = 4x^2 – 11x – 2 over left( x + 2 right)left( x – 1 right)) Đk: (x ne 1;x ne – 2) (eqalign& Leftrightarrow x + 2 over 1 – x = 11x + 2 – 4x^2 over left( x + 2 right)left( x – 1 right) cr & Leftrightarrow left( x + 2 right)^2 = 11x + 2 – 4x^2 cr & Leftrightarrow x^2 + 4x + 4 = 11x + 2 – 4x^2 cr & Leftrightarrow 5x^2 – 7x + 2 = 0 cr ) Phương trình có dạng: (a + b + c = 0 Rightarrow 5 + left( – 7 right) + 2 = 0) (x_1 = 1;x_2 = 2 over 5) x1 = 1 không thỏa mãn thị hiếu Đk: loại. Vậy phương trình có một nghiệm: (x = 2 over 5) d) (x^2 + 14x over x^3 + 8 = x over x + 2) Đk: (x ne – 2) (eqalign& Leftrightarrow x^2 + 14x over left( x + 2 right)left( x^2 – 2x + 4 right) = x over x + 2 cr & Leftrightarrow x^2 + 14x = xleft( x^2 – 2x + 4 right) cr & Leftrightarrow x^2 + 14x = x^3 – 2x^2 + 4x cr & Leftrightarrow x^3 – 3x^2 – 10x = 0 cr & Leftrightarrow xleft( x^2 – 3x – 10 right) = 0 cr & Rightarrow left[ matrixx = 0 cr x^2 – 3x – 10 = 0 cr right. cr ) (eqalign& x^2 – 3x – 10 = 0 cr & Delta = left( – 3 right)^2 – 4.1.left( – 10 right) = 9 + 40 = 49 > 0 cr & sqrt Delta = sqrt 49 = 7 cr & x_1 = 3 + 7 over 2.1 = 10 over 2 = 5 cr & x_2 = 3 – 7 over 2.1 = – 4 over 2 = – 2 cr ) Giá trị x = -2 không thỏa mãn thị hiếu Đk: loại. Vậy phương trình có hai nghiệm: (x_1 = 0;x_2 = 5) Câu 69 trang 63 Sách bài tập (SBT) Toán 9 tập 2 Giải những phương trình trùng phương a) (x^4 + 2x^2 – x + 1 = 15x^2 – x – 35) b) (2x^4 + x^2 – 3 = x^4 + 6x^2 + 3) c) (3x^4 – 6x^2 = 0) d) (5x^4 – 7x^2 – 2 = 3x^4 – 10x^2 – 3) Giải a) (eqalign& x^4 + 2x^2 – x + 1 = 15x^2 – x – 35 cr & Leftrightarrow x^4 + 2x^2 – x + 1 – 15x^2 + x + 35 = 0 cr & Leftrightarrow x^4 – 13x^2 + 36 = 0 cr ) Đặt (x^2 = t;t ge 0) Ta có phương trình: (t^2 – 13t + 36 = 0) (eqalign& Delta = left( – 13 right)^2 – 4.1.36 = 169 – 144 = 25 > 0 cr & sqrt Delta = sqrt 25 = 5 cr & t_1 = 13 + 5 over 2.1 = 18 over 2 = 9 cr & t_2 = 13 – 5 over 2.1 = 8 over 2 = 4 cr & x^2 = 9 Leftrightarrow x = pm 3 cr & x^2 = 4 Leftrightarrow x = pm 2 cr ) Vậy phương trình có 4 nghiệm: (x_1 = 3;x_2 = – 3;x_3 = 2;x_4 = – 2) b) (eqalign& 2x^4 + x^2 – 3 = x^4 + 6x^2 + 3 cr & Leftrightarrow x^4 – 5x^2 – 6 = 0 cr ) Đặt (x^2 = t Rightarrow t ge 0,) ta có phương trình: (t^2 – 5t – 6 = 0) Phương trình có dạng: (a – b + c = 0;1 – left( – 5 right) + left( – 6 right) = 0) (t_1 = – 1;t_2 = – – 6 over 1 = 6) t1 = -1 < 0: loại (x^2 = 6 Leftrightarrow x = pm sqrt 6 ) Vậy phương trình có 2 nghiệm: (x_1 = sqrt 6 ;x_2 = – sqrt 6 ) c) (eqalign& 3x^4 – 6x^2 = 0 cr & Leftrightarrow 3x^2left( x^2 – 2 right) = 0 cr & Leftrightarrow left[ matrix3x^2 = 0 cr x^2 – 2 = 0 cr Leftrightarrow left[ matrixx = 0 cr x = pm sqrt 2 cr right. right. cr ) Vậy phương trình có 3 nghiệm: (x_1 = 0;x_2 = sqrt 2 ;x_3 = – sqrt 2 ) d) (5x^4 – 7x^2 – 2 = 3x^4 – 10x^2 – 3 Leftrightarrow 2x^4 + 3x^2 + 1 = 0) Đặt (x^2 = t Rightarrow t ge 0,) ta có phương trình: (2t^2 + 3t + 1 = 0) Phương trình có dạng: (a – b + c = 0;2 – 3 + 1 = 0) (t_1 = – 1;t_2 = – 1 over 2) Cả hai giá trị t1 và t2 đều nhỏ hơn 0: loại. Vậy phương trình đã cho vô nghiệm Câu 70 trang 63 Sách bài tập (SBT) Toán 9 tập 2 Giải những phương trình sau bằng phương pháp đặt ẩn phụ: a) (left( x^2 – 2x right)^2 – 2x^2 + 4x – 3 = 0) b) (3sqrt x^2 + x + 1 – x = x^2 + 3) Giải a) (eqalign& left( x^2 – 2x right)^2 – 2x^2 + 4x – 3 = 0 cr & Leftrightarrow left( x^2 – 2x right)^2 – 2left( x^2 – 2x right) – 3 = 0 cr ) Đặt (x^2 – 2x = t,) ta có phương trình: (t^2 – 2t – 3 = 0) Phương trình có dạng: (a – b + c = 0;1 – left( – 2 right) + left( – 3 right) = 0) (t_1 = – 1;t_2 = – – 3 over 1 = 3) Ta có: (eqalign& x^2 – 2x = – 1 Leftrightarrow x^2 – 2x + 1 = 0 cr & Delta ‘ = left( – 1 right)^2 – 1.1 = 1 – 1 = 0 cr ) Phương trình có nghiệm số kép: x1 = x2 = 1 (x^2 – 2x = 3 Leftrightarrow x^2 – 2x – 3 = 0) Phương trình có dạng: (a – b + c = 0;1 – left( – 2 right) + left( – 3 right) = 0) (x_1 = – 1;x_2 = – – 3 over 1 = 3) Vậy phương trình có 3 nghiệm: (x_1 = 1;x_2 = – 1;x_3 = 3) b) (3sqrt x^2 + x + 1 – x = x^2 + 3,) ta có: (x^2 + x + 1 = left( x + 1 over 2 right)^2 + 3 over 4 ge 0) ( Leftrightarrow x^2 + x + 1 – 3sqrt x^2 + x + 1 + 2 = 0) Đặt (sqrt x^2 + x + 1 = t Rightarrow t ge 0,) ta có phương trình: (t^2 – 3t + 2 = 0) Phương trình có dạng: (a + b + c = 0;1 + left( – 3 right) + 2 = 0) (t_1 = 1;t_2 = 2) (eqalign& Rightarrow sqrt x^2 + x + 1 = 1 Rightarrow x^2 + x + 1 = 1 cr & Leftrightarrow xleft( x + 1 right) = 0 cr & Rightarrow left[ matrixx = 0 cr x + 1 = 0 cr Leftrightarrow left[ matrixx = 0 cr x = – 1 cr right. right. cr ) (eqalign& sqrt x^2 + x + 1 = 2 Rightarrow x^2 + x + 1 = 4 cr & Rightarrow x^2 + x – 3 = 0 cr & Delta = 1^2 – 4.1.left( – 3 right) = 1 + 12 = 13 > 0 cr & sqrt Delta = sqrt 13 cr & x_1 = – 1 + sqrt 13 over 2.1 = – 1 + sqrt 13 over 2 cr & x_2 = – 1 – sqrt 13 over 2.1 = – 1 – sqrt 13 over 2 cr ) Vậy phương trình có 4 nghiệm: (x_1 = 0;x_2 = 1;x_3 = – 1 + sqrt 13 over 2;x_4 = – 1 – sqrt 13 over 2) Giaibaitap.me Page 6Câu 71 trang 63 Sách bài tập (SBT) Toán 9 tập 2 Cho phương trình: (x^2 – 2left( m + 1 right)x + m^2 + m – 1 = 0) a) Tìm những giá trị của m để phương trình có nghiệm. b) Trong trường hợp phương trình có nghiệm là x1, x2 hãy tính theo m: (x_1 + x_2;x_1x_2;x_1^2 + x_2^2) Giải a) Phương trình có nghiệm khi và chỉ khi (Delta ‘ ge 0) (eqalign& Delta ‘ = left[ – left( m + 1 right) right]^2 – 1left( m^2 + m – 1 right) cr & = m^2 + 2m + 1 – m^2 – m + 1 = m + 2 cr & Delta ‘ ge 0 Rightarrow m + 2 ge 0 Leftrightarrow m ge – 2 cr ) Vậy với m ≥ -2 thì phương trình đã cho có nghiệm. b) Phương trình có 2 nghiệm x1 và x2, theo hệ thức Vi-ét ta có: (eqalign& x_1 + x_2 = 2left( x + 1 right) over 1 = 2m + 2 cr & x_1x_2 = m^2 + m – 1 over 1 = m^2 + m – 1 cr & x_1^2 + x_2^2 = left( x_1 + x_2 right)^2 – 2x_1x_2 cr & = left( 2m + 2 right)^2 – 2left( m^2 + m – 1 right) cr & = 4m^2 + 8m + 4 – 2m^2 – 2m + 2 cr & = 2m^2 + 6m + 6 cr ) Câu 72 trang 63 Sách bài tập (SBT) Toán 9 tập 2 Tìm hai số biết tổng của chúng bằng 10 và tích của chúng bằng -10. Giải Hai số có tổng bằng 10 và tích bằng -10 nó là nghiệm của phương trình: (eqalign& x^2 – 10x – 10 = 0 cr & Delta ‘ = left( – 5 right)^2 – 1.left( – 10 right) = 25 + 10 = 35 > 0 cr & sqrt Delta ‘ = sqrt 35 cr & x_1 = 5 + sqrt 35 over 1 = 5 + sqrt 35 cr & x_2 = 5 – sqrt 35 over 1 = 5 – sqrt 35 cr ) Câu 73 trang 63 Sách bài tập (SBT) Toán 9 tập 2 Một đội thợ mỏ phải khai thác 216 tấn than trong thuở nào hạn nhất định. Ba ngày đầu mỗi ngày đội khai thác theo như đúng định mức. Sau đó mỗi ngày họ đều khai thác vượt định mức 8 tấn. Do đó họ khai thác được 232 tấn và xong trước thời hạn một ngày. Hỏi theo kế hoạch mỗi ngày đội thợ phải khai thác bao nhiêu tấn than? Giải Gọi lượng than mà mỗi đội dự tính khai thác mỗi ngày theo kế hoạch là x (tấn) Điều kiện: x > 0 Thời gian dự tính khai thác là (216 over x) ngày Lượng than khai thác 3 ngày đầu là 3x tấn Lượng than khai thác trong những ngày còn sót lại là (232 – 3x) (tấn) Mỗi ngày sau đội khai thác được x + 8 tấn Thời gian đội khai thác 232 – 3x tấn là (232 – 3x over x + 8) ngày. Ta có phương trình: (eqalign& 216 over x – 1 = 3 + 232 – 3x over x + 8 cr & Rightarrow 216left( x + 8 right) – xleft( x + 8 right) = 3xleft( x + 8 right) + left( 232 – 3x right)x cr & Leftrightarrow 216x + 1728 – x^2 – 8x = 3x^2 + 24x + 232x – 3x^2 cr & Leftrightarrow x^2 + 48x – 1728 = 0 cr & Delta ‘ = 24^2 – 1.left( – 1728 right) = 576 + 1728 = 2304 > 0 cr & sqrt Delta ‘ = sqrt 2304 = 48 cr & x_1 = – 24 + 48 over 1 = 24 cr & x_2 = – 24 – 48 over 1 = – 72 cr ) x2 = -72 < 0 không thỏa mãn thị hiếu Đk: loại. Vậy theo kế hoạch mỗi ngày đội khai thác 24 tấn than. Câu 74 trang 63 Sách bài tập (SBT) Toán 9 tập 2 Khoảng cách giữa hai bến sông A và B là 30km. Một ca nô đi từ A đến B, nghỉ 40 phút ở B rồi lại trở về bến A. Thời gian Tính từ lúc lúc đi đến lúc trở về đến A là 6 giờ. Tính vận tốc của ca nô khi nước yên lặng, biết rằng vận tốc của làn nước là 30km/h. Giải Gọi vận tốc ca nô khi nước yên lặng là x (km/h); Đk: x > 3 Thì vận tốc lúc đi xuôi dòng là x + 3 (km/h) Vận tốc ca nô đi ngược dòng là x – 3 (km/h) Thời gian đi xuôi dòng là (30 over x + 3) giờ Thời gian đi ngược dòng là (30 over x – 3) giờ Ta có phương trình: (eqalign& 30 over x + 3 + 30 over x – 3 = 16 over 3 cr & Rightarrow 90left( x – 3 right) + 90left( x + 3 right) = 16left( x + 3 right)left( x – 3 right) cr & Leftrightarrow 90x – 270 + 90x + 270 = 16x^2 – 144 cr & Leftrightarrow 16x^2 – 180x – 144 = 0 cr & Leftrightarrow 4x^2 – 45x – 36 = 0 cr & Delta = left( – 45 right)^2 – 4.4.left( – 36 right) = 2025 + 675 = 2601 > 0 cr & sqrt Delta = sqrt 2601 = 51 cr & x_1 = 45 + 51 over 2.4 = 96 over 8 = 12 cr & x_2 = 45 – 51 over 2.4 = – 6 over 8 = – 3 over 4 cr ) (x_2 = – 3 over 4 < 0) không thỏa mãn thị hiếu Đk: loại. Vậy vận tốc ca nô khi nước yên lặng là 12 km/h. Giaibaitap.me Page 7Câu IV.4 trang 64 Sách bài tập (SBT) Toán 9 tập 2 Cho phương trình: (x^2 + px + 1 = 0) có hai nghiệm. Xác định p. biết rằng tổng những bình phương của hai nghiệm bằng 254. Giải Cho phương trình: (x^2 + px + 1 = 0) Phương trình đã cho có hai nghiệm thì (Delta ge 0) (eqalign & Delta = p.^2 – 4 cr & Rightarrow p.^2 – 4 ge 0 Leftrightarrow p.^2 ge 4 Leftrightarrow left[ matrix p. ge 2 cr p. le – 2 cr right. cr ) Theo hệ thức Vi-ét ta có: (x_1 + x_2 = – p.;x_1x_2 = 1) Theo bài ra ta có: (x_1^2 + x_2^2 = 254) (eqalign & Leftrightarrow left( x_1 + x_2 right)^2 – 2x_1x_2 = 254 cr & Leftrightarrow p.^2 – 2.1 = 254 cr & Leftrightarrow p.^2 = 256 cr & Leftrightarrow left[ matrix p. = 16 cr p. = – 16 cr right. cr ) Cả hai giá trị đều thỏa mãn thị hiếu Đk. Vậy với p. = 16 hoặc p. = -16 thì phương trình có hai nghiệm thỏa mãn thị hiếu (x_1^2 + x_2^2 = 254) Câu IV.5 trang 64 Sách bài tập (SBT) Toán 9 tập 2 Cho phương trình: (x^4 – 13x^2 + m = 0). Tìm những giá trị của m để phương trình: a) Có 4 nghiệm phân biệt b) Có 3 nghiệm phân biệt c) Có 2 nghiệm phân biệt d) Có một nghiệm e) Vô nghiệm. Giải Cho phương trình: (x^4 – 13x^2 + m = 0) (1) Đặt (x^2 = t Rightarrow t ge 0,) ta có phương trình: (t^2 – 13t + m = 0) (2) (Delta = 169 – 4m) a) Phương trình (1) có 4 nghiệm phân biệt khi phương trình (2) có hai nghiệm số dương khi (left{ {matrix Delta = 169 – 4m > 0 cr t_1t_2 = m > 0 cr t_1 + t_2 = 13 > 0 cr Leftrightarrow left matrixm < 169 over 4 cr m > 0 cr Leftrightarrow 0 < m < 169 over 4 right. right.) b) Phương trình (1) có ba nghiệm phân biệt khi phương trình (2) có một nghiệm số dương và 1 nghiệm bằng 0 khi: (left{ {matrix Delta = 169 – 4m > 0 cr t_1 + t_2 = 13 > 0 cr t_1.t_2 = m = 0 cr Leftrightarrow left matrixm < 169 over 4 cr m = 0 cr right. Leftrightarrow m = 0 right.) c) Phương trình (1) có hai nghiệm phân biệt khi phương trình (2) có nghiệm kép hoặc có một nghiệm dương và một nghiệm âm. Phương trình (2) có một nghiệm số kép khi và chỉ khi (Delta = 169 – 4m = 0) ( Leftrightarrow m = 169 over 4 Rightarrow t_1 = t_2 = 13 over 2) Phương trình (2) có một nghiệm số dương và một nghiệm số âm khi (left{ {matrix Delta = 169 – 4m > 0 cr t_1.t_2 = m < 0 cr Leftrightarrow left matrixm < 169 over 4 cr m < 0 cr Leftrightarrow m < 0 right. right.) Vậy với (m = 169 over 4) hoặc m < 0 thì phương trình (1) có 3 nghiệm phân biệt. d) Phương trình (1) có một nghiệm khi phương trình (2) có một nghiệm số kép bằng 0 hoặc phương trình (2) có một nghiệm bằng 0 và một nghiệm số âm. Ta thấy phương trình (2) có nghiệm số kép (t_1 = t_2 = 13 over 2 ne 0) Nếu phương trình (2) có một nghiệm t1 = 0. Theo hệ thức Vi-ét ta có: (t_1 + t_2 = 13 Rightarrow t_2 = 13 – t_1 = 13 – 0 = 13 > 0) Vậy không tồn tại giá trị nào của m để phương trình (1) chỉ có một nghiệm. e) Phương trình (1) vô nghiệm khi phương trình (2) có 2 nghiệm số âm hoặc vô nghiệm. Nếu phương trình (2) có 2 nghiệm âm thì theo hệ thức Vi-ét ta có: (t_1 + t_2 = 13 > 0) vô lý Vậy phương trình (1) vô nghiệm khi phương trình (2) vô nghiệm. Suy ra: (Delta = 169 – 4m < 0 Leftrightarrow m > 169 over 4) Giaibaitap.me Page 8Câu IV.1 trang 64 Sách bài tập (SBT) Toán 9 tập 2 Cho hàm số (y = – 3x^2). Khẳng định nào sau đấy là đúng? A) Khi 0 < x < 15, hàm số đồng biến B) Khi -1 < x < 1, hàm số đồng biến C) Khi -15 < x < 0, hàm số đồng biến D) Khi -15 < x < 1, hàm số đồng biến Giải Cho hàm số: (y = – 3x^2). Khẳng định sau đấy là đúng. Chọn C) Khi -15 < x < 0, hàm số đồng biến. Câu IV.2 trang 64 Sách bài tập (SBT) Toán 9 tập 2 Muốn tìm hai số lúc biết tổng của chúng bằng S, tích của chúng bằng P thì ta giải phương trình nào tại đây? A) (x^2 + Sx + P = 0) B) (x^2 – Sx + P = 0) C) (x^2 – Sx – P = 0) D) (x^2 + Sx – P = 0) Giải Muốn tìm hai số lúc biết tổng bằng S, tích của chúng bằng P thì ta phải giải phương trình Chọn B) (x^2 – Sx + P = 0) Câu IV.3 trang 64 Sách bài tập (SBT) Toán 9 tập 2 Giải những phương trình: a) (x^3 + 4x^2 + x – 6 = 0) b) (x^3 – 2x^2 – 5x + 6 = 0) c) (2x^4 + 2sqrt 2 x^3 + left( 1 – 3sqrt 2 right)x^2 – 3x – 4 = 0) d) (left( 2x^2 + 7x – 8 right)left( 2x^2 + 7x – 3 right) – 6 = 0) Giải a) (eqalign& x^3 + 4x^2 + x – 6 = 0 cr & Leftrightarrow x^3 + 2x^2 + 2x^2 + 4x – 3x – 6 = 0 cr & Leftrightarrow x^2left( x + 2 right) + 2xleft( x + 2 right) – 3left( x + 2 right) = 0 cr & Leftrightarrow left( x + 2 right)left( x^2 + 2x – 3 right) = 0 cr & Leftrightarrow left[ matrixx + 2 = 0 cr x^2 + 2x – 3 = 0 cr right. cr & x + 2 = 0 Leftrightarrow x = – 2 cr ) (x^2 + 2x – 3 = 0). Phương trình có dạng: (a + b + c = 0;1 + 2 + left( – 3 right) = 0) (x_1 = 1;x_2 = – 3 over 1 = – 3) Vậy phương trình có 3 nghiệm: (x_1 = – 2;x_2 = 1;x_3 = – 3) b) (eqalign& x^3 – 2x^2 – 5x + 6 = 0 cr & Leftrightarrow x^3 – x^2 – x^2 + x – 6x + 6 = 0 cr & Leftrightarrow x^2left( x – 1 right) – xleft( x – 1 right) – 6left( x – 1 right) = 0 cr & Leftrightarrow left( x – 1 right)left( x^2 – x – 6 right) = 0 cr & Leftrightarrow left[ matrixx – 1 = 0 cr x^2 – x – 6 = 0 cr right. cr & x – 1 = 0 Leftrightarrow x = 1 cr & x^2 – x – 6 = 0 cr & Delta = left( – 1 right)^2 – 4.1.left( – 6 right) = 1 + 24 = 25 > 0 cr & sqrt Delta = sqrt 25 = 5 cr & x_1 = 1 + 5 over 2.1 = 3 cr & x_2 = 1 – 5 over 2.1 = – 2 cr ) Vậy phương trình đã cho có 3 nghiệm: (x_1 = 1;x_2 = 3;x_3 = – 2) c) (eqalign& 2x^4 + 2sqrt 2 x^3 + left( 1 – 3sqrt 2 right)x^2 – 3x – 4 = 0 cr & Leftrightarrow 2x^4 + 2sqrt 2 x^3 + x^2 – 3sqrt 2 x^2 – 3x – 4 = 0 cr & Leftrightarrow left( sqrt 2 x^2 + x right)^2 – 3left( sqrt 2 x^2 + x right) – 4 = 0 cr ) Đặt (sqrt 2 x^2 + x = t,) ta có phương trình: $t^2 – 3t – 4 = 0) Phương trình có dạng: (a – b + c = 0;1 – left( – 3 right) + left( – 4 right) = 0) (t_1 = – 1;t_2 = – – 4 over 1 = 4) Với (t = – 1 Rightarrow sqrt 2 x^2 + x + 1 = 0) (Delta = 1 – 4.sqrt 2 .1 = 1 – 4sqrt 2 < 0) phương trình vô nghiệm Với (t = 4 Rightarrow sqrt 2 x^2 + x = 4 Leftrightarrow sqrt 2 x^2 + x – 4 = 0) (eqalign& Delta = 1^2 – 4.sqrt 2 .left( – 4 right) = 1 + 16sqrt 2 > 0 cr & sqrt Delta = sqrt 1 + 16sqrt 2 cr & x_1 = – 1 + sqrt 1 + 16sqrt 2 over 2.sqrt 2 = – sqrt 2 + sqrt 2 + 32sqrt 2 over 4 cr & x_2 = – 1 – sqrt 1 + 16sqrt 2 over 2.sqrt 2 = – sqrt 2 – sqrt 2 + 32sqrt 2 over 4 cr ) Phương trình đã cho có hai nghiệm. d) (eqalign& left( 2x^2 + 7x – 8 right)left( 2x^2 + 7x – 3 right) – 6 = 0 cr & Leftrightarrow left[ left( 2x^2 + 7x – 3 right) – 5 right]left( 2x^2 + 7x – 3 right) – 6 = 0 cr & Leftrightarrow left( 2x^2 + 7x – 3 right)^2 – 5left( 2x^2 + 7x – 3 right) – 6 = 0 cr ) Đặt (2x^2 + 7x – 3 = t,) ta có phương trình: (t^2 – 5t – 6 = 0) Phương trình có dạng (a – b + c = 0;1 – left( – 5 right) + left( – 6 right) = 0) (t_1 = – 1;t_2 = – – 6 over 1 = 6) Với t = -1 ta có: (eqalign& 2x^2 + 7x – 3 = – 1 Leftrightarrow 2x^2 + 7x – 2 = 0 cr & Delta = 7^2 – 4.2.left( – 2 right) = 49 + 16 = 65 > 0 cr & sqrt Delta = sqrt 65 cr & x_1 = – 7 + sqrt 65 over 2.2 = – 7 + sqrt 65 over 4 cr & x_2 = – 7 – sqrt 65 over 2.2 = – 7 – sqrt 65 over 4 cr ) Với t = 6, ta có: (2x^2 + 7x – 3 = 6 Leftrightarrow 2x^2 + 7x – 9 = 0) Phương trình có dạng: (a + b + c = 0;2 + 7 + left( – 9 right) = 0) (x_1 = 1;x_2 = – 9 over 2) Vậy phương trình đã cho có 4 nghiệm: (x_1 = – 7 + sqrt 65 over 4;x_2 = – 7 – sqrt 65 over 4;x_3 = 1;x_4 = – 9 over 2) Giaibaitap.me Page 9
Page 10Câu 4 trang 99 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Hai tiếp tuyến tại A, B của đường tròn (O, R) cắt nhau taị M. Biết OM=2R. Tính số đo góc ở tâm AOB? Giải
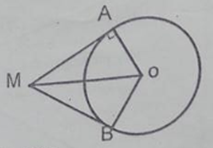 (MA bot OA) (tính chất tiếp tuyến) Trong ∆MAO có (widehat OAM = 90^0) (coswidehat AOM = OA over OM = R over 2R = 1 over 2) ( Rightarrow widehat AOM = 60^0) (widehat AOM = 1 over 2widehat AOB) (tính chất 2 tiếp tuyến giao nhau) ( Rightarrow widehat AOB = 2widehat AOM = 120^0) Câu 5 trang 99 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho đường tròn (O, R), đường kính AB. Gọi C là yếu tố ở chính giữa của cung AB. Vẽ dây cung AB. Vẽ dây CD dài bằng R. Tính góc ở tâm DOB. Có mấy đáp số? Giải 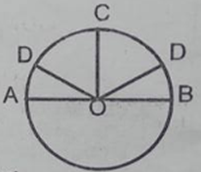 Điểm D có 2 trường hợp : Nếu điểm D nằm trong lòng C và B Ta có C điểm ở chính giữa của cung AB số đo cung BC = số đo cung AC = 900 CD = R (gt) Suy ra : OC = OD = CD = R ( Rightarrow Delta OCrmD) đều ( Rightarrow widehat COD = 60^0) ( Rightarrow ) sđ cung CD = sđ cung COD = 600 ( Rightarrow ) sđ cung BD = sđ cung BC – sđ cung CB = $90^0 – 60^0 = 30^0) (widehat BOD) = sđ cung BD = 300 Nếu C nằm trong lòng B và D ta có : CD = OC = OD = R ( Rightarrow Delta OCD) đều ( Rightarrow widehat COD = 60^0) sđ cung CD = sđ cung COD = 600 sđ cung BD = sđ cung BC + sđ cung CD= (90^0 + 60^0 = 150^0) (widehat BOD) = sđ cung BD = 1500 Câu 6 trang 99 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho hai tuyến phố đường tròn (O; R) và (O’;R’) cắt nhau tại A, B. Hãy so sánh R và R’ trong những trường hợp sau: a) Số đo cung nhỏ AB của (O; R) to nhiều hơn số đo cung nhỏ AB của (O’; R’). b) Số đo cung lớn AB của (O; R) nhỏ hơn số đo cung lớn AB của (O; R’). c) Số đo hai cung nhỏ bằng nhau Giải
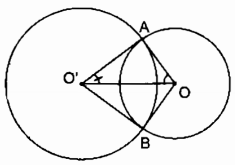 a) Trong (O; R) ta có: (widehat AOB) = sđ cung AB (nhỏ) Trong (O’; R) ta có: (widehat AO’B) = sđ cung AB (nhỏ) Vì số đo cung AB nhỏ của (O; R) to nhiều hơn số đo cung AB nhỏ của (O’; R’) Suy ra: (widehat AOB > widehat AO’B) (1) (Delta AOO’ = Delta BOO’) (cạnh – cạnh – cạnh) ( Rightarrow widehat AOO’ = widehat BOO’ = 1 over 2widehat AOB) (2) (widehat AO’O = widehat BO’O = 1 over 2widehat AO’B) (3) Từ (1), (2) và (3) suy ra: (widehat AOO’ > widehat AO’O) Trong (Delta AOO’) ta có: (widehat AOO’ > widehat AO’O) Suy ra: O’A > OA hay R’ > R Trường hợp hình thứ hai, ta lấy đối xứng của (O) qua trục AB ta có kết quả như hình trên.
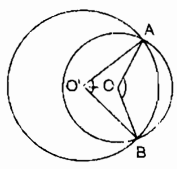 b) Trong (O; R) số đo cung lớn AB cộng với số đo cung nhỏ AB bằng 3600 Mà số đo cung lớn AB của (O;R) nhỏ hơn số đo cung lớn AB của (O’; R’) Suy ra số đo cung nhỏ AB của (O; R) to nhiều hơn số đo cung nhỏ của (O’; R’) Chứng minh tương tự câu a ta có: R > R’. c) Số đo hai cung nhỏ của (O; R) và (O’; R’) bằng nhau ( Rightarrow widehat AOB = widehat AO’B) Suy ra: (widehat AOO’ = widehat AO’O Rightarrow Delta AOO’) cân tại A nên OA = OA’ hay R = R’. Giaibaitap.me Page 11Câu 7 trang 99 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho hai tuyến phố tròn (O) và (O’) cắt nhau tại A, B. Đường phân giác của góc OBO’ cắt những đường tròn (O), (O’) tương ứng tại C, D. Hãy so sánh những góc ở tâm BOC và BO’D. Hướng dẫn. Sử dụng những tam giác cân OBC, O’BD. Giải
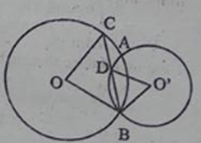 Trong (O) ta có: (Delta OBC) cân tại O (vì OB = OC nửa đường kính) ( Rightarrow widehat BOC = 180^0 – 2.widehat OBC) (1) Trong (O’) ta có (Delta BO’D) cân tại O’ (vì O’D = O’D nửa đường kính) ( Rightarrow widehat BO’D = 180^0 – 2.widehat O’BD) (2) (widehat OBC = widehat O’BD) (vì BC là phân giác của (widehat OBO’)) (3) Từ (1), (2) và (3) suy ra: (widehat BOC = widehat BO’D). Câu 8 trang 100 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Trên một đường tròn, có cung AB bằng 1400, cung AD nhận B làm điểm ở chính giữa, cung CB nhận A là yếu tố ở chính giữa. Tính số đo cung nhỏ CD và cung lớn CD. Giải
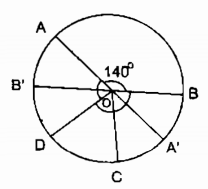 Ta có: cung AB = cung BD = cung AC (gt) ( Rightarrow widehat AOB = widehat BOD = widehat AOC = 180^0) Kẻ đường kính AA’, BB’ ta có: (widehat AOB + widehat AOB’ = 180^0) (hai góc kề bù) ( Rightarrow widehat AOB’ = 180^0 – widehat AOB = 180^0 – 140^0 = 40^0) Suy ra: (widehat BOA’ = widehat AOB’ = 40^0) (hai góc đối đỉnh) (widehat B’OD + widehat BOD = 180^0) (hai góc kề bù) ( Rightarrow widehat B’OD = 180^0 – widehat BOD = 180^0 – 140^0 = 40^0) (widehat AOC = widehat AOB’ + widehat B’OD + widehat DOC) ( Rightarrow widehat DOC = widehat AOC – widehat AOB’ – widehat B’OD = 140^0 – 40^0 – 40^0 = 60^0) sđ cung CD (nhỏ) = (widehat COD = 60^0) sđ cung CD (lớn) = sđ cung CD (nhỏ) = 3600 – 600 = 3000 Câu 9 trang 100 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho C là một điểm nằm trên cung lớn AB của đường tròn (O). Điểm C của cung lớn AB thành hai cung AC và CB. Chứng minh rằng cung lớn AB có sđ cung AB = sđ cung AC = sđ cung CB. Hướng dẫn: Xét 3 trường hợp: a) Tia OC nằm trong góc đối đỉnh của góc ở tâm AOB. b) Tia OC trùng với tia đối của một cạnh của góc ở tâm AOB c) Tia OC nằm trong một góc kề bù với góc ở tâm AOB Giải 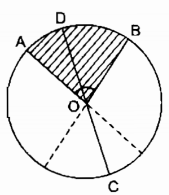 a) Trường hợp tia OC nằm trong góc đối đỉnh với (widehat AOB) Kẻ đường kính CD Suy ra: OD nằm trong lòng OA và OB nên điểm D nằm trên cung nhỏ cung AB ( Rightarrow ) sđ cung AD (nhỏ) + sđ cung BD (nhỏ) = sđ cung AB (nhỏ) (1) Vì OA nằm trong lòng OC và OD nên điểm A nằm trên cung nửa đường tròn CD. ( Rightarrow ) sđ cung AD (nhỏ) + sđ cung AC (nhỏ) = 1800 (2) Vì OB nằm trong lòng OC và OD nên điểm B nằm trên cung nửa đường tròn CD. ( Rightarrow ) sđ cung BD (nhỏ) + sđ cung BC (nhỏ) = 1800 (3) Cộng từng vế (2) và (3): sđ cung AD (nhỏ) + sđ cung AC (nhỏ) + sđ cung BD (nhỏ) + sđ cung BC (nhỏ) = 3600 (4) Từ (1) và (4) suy ra: sđ cung AC (nhỏ) + sđ cung BC (nhỏ) + sđ cung AB (nhỏ) = 3600 ( Rightarrow ) sđ cung AC (nhỏ) + sđ cung BC (nhỏ) = 3600 – sđ cung AB (nhỏ) Mà 3600 – sđ cung AB (nhỏ) = sđ cung AD (lớn) Vậy với cung lớn AB ta có: sđ cung AB = sđ cung AC + sđ cung BC b) 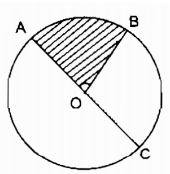 Trường hợp tia OC trùng với tia đối của một cạnh của góc ở tâm AOB ta có: (widehat AOB + widehat BOC = 180^0); $widehat AOC = 180^0) ( Rightarrow widehat AOB + widehat BOC + widehat AOC = 360^0) ( Rightarrow widehat AOC + widehat BOC = 360^0 – widehat AOB) Suy ra: sđ cung AB + sđ cung BC (nhỏ) = 3600 – sđ cung AB (nhỏ) Vậy với cung lớn AB ta có: sđ cung AB = sđ cung AC (nhỏ) + sđ cung BC c) 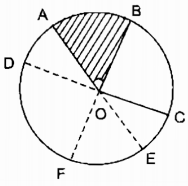 Trong hợp tia OC nằm trong góc kề bù với góc ở tâm AOB, kẻ đường kính AE. Theo trường hợp b ta có: sđ cung AB (lớn) = sđ cung AE (nhỏ) + sđ cung BE (nhỏ) Ta xét trường hợp C nằm trên cung nhỏ EB: sđ cung EB (nhỏ) = sđ cung EC (nhỏ) + sđ cung CB (nhỏ) ( Rightarrow ) sđ cung AB (lớn) = sđ cung AE + sđ cung EC (nhỏ) + sđ cung CB (nhỏ) Theo kết quả trường hợp b ta có: sđ cung AE + sđ cung EC (nhỏ)= sđ cung AC (lớn) Vậy với cung AB lớn ta có: sđ cung AB = sđ cung AC + sđ cung CB Trong trường hợp OC nằm trên góc so với góc ở tâm (widehat BOE) chứng tỏ tương tự. Trong trường hợp OC nằm trên góc đối đỉnh với góc ở tâm (widehat AOB) chứng tỏ ở trường hợp a. Giaibaitap.me Page 12Câu 1.1 trang 100 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho hình bs.4. Biết (overparenDOA)= 1200, OA vuông góc với OC, OB vuông góc với OD. a) Đọc tên những gốc ở tâm có số đo nhỏ hơn 1800. b) Cho biết số đo của mỗi góc ở tâm tìm kiếm được ở câu trên. c) Cho biết tên của những cặp cung có số đo bằng nhau (nhỏ hơn 1800). d) So sánh hai cung nhỏ AB và BC. Giải 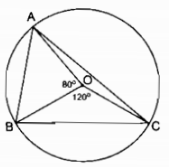
a) Các góc ở tâm có số đo nhỏ hơn 1800 là: (widehat AOB,widehat AOC,widehat AOD,widehat BOC,widehat BOD,widehat COD) b) (OA bot OC Rightarrow widehat AOC = 90^0) (OB bot OD Rightarrow widehat BOD = 90^0) (widehat AOB + widehat BOD = widehat AOD) ( Rightarrow widehat AOB = widehat AOD – widehat BOD = 120^0 – 90^0 = 30^0) (widehat AOC + widehat COD = widehat AOD) ( Rightarrow widehat COD = widehat AOD – widehat AOC = 120^0 – 90^0 = 30^0) (widehat AOB + widehat BOC = widehat AOC) ( Rightarrow widehat BOC = widehat AOC – widehat AOB = 90^0 – 30^0 = 60^0) c) Các cung có số đo bằng nhau nhỏ hơn 1800 là: (overparenAB) = (overparenCD); (overparenAC) = (overparenBD) d) sđ (overparenAB)=( = widehat AOB = 30^0) sđ (overparenBC)( = widehat BOC = 60^0) Suy ra: sđ (overparenBC) gấp hai sđ (overparenAB) Câu 1.2 trang 100 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho đường tròn tâm O đường kính AB. Các điểm C, D, E cùng thuộc một cung AB sao cho sđ (overparenBC) = sđ (overparenBA) ; sđ (overparenBD) = (1 over 2) sđ (overparenBA); sđ (overparenBE) = (2 over 3) sđ (overparenBA). a) Đọc tên những góc ở tâm có số đo không to nhiều hơn 1800. b) Cho biết số đo của mỗi góc ở tâm tìm kiếm được ở câu trên. c) Cho biết tên của những cặp cung có số đo bằng nhau (nhỏ hơn 1800). d) So sánh hai cung nhỏ AE và BC. Giải 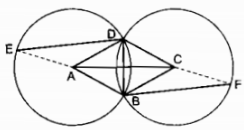 a) Các góc ở tâm có số đo không thật 1800 là: (widehat AOB,widehat AOC,widehat AOD,widehat AOE,widehat BOC,widehat BOD,) (widehat BOE,widehat COD,widehat COE,widehat DOE) b) (widehat AOB = 180^0) sđ (overparenAB) = 1800 Ta có: sđ (overparenBC) = ( = 1 over 6) sđ (overparenAB) = (1 over 6.180^0) = 300 ( Rightarrow widehat BOC = ) sđ (overparenBC) = 300 Ta có: sđ (overparenBD) ( = 1 over 2)sđ (overparenAB) = (1 over 2.180^0 = 90^0) ( Rightarrow widehat BOD = )sđ (overparenBD) = (90^0) Ta có: sđ (overparenBE) ( = 2 over 3) sđ (overparenBA) ( = 2 over 3.180^0 = 120^0) ( Rightarrow widehat BOE = ) sđ (overparenBE) = 1200 (widehat BOC + widehat COE = widehat BOE) ( Rightarrow widehat COE = widehat BOE – widehat BOC) ( = 120^0 – 30^0 = 90^0) (widehat AOE + widehat BOE = widehat AOB) ( Rightarrow widehat AOE = widehat AOB – widehat BOE) ( = 180^0 – 120^0 = 60^0) (widehat AOD = widehat BOD = 1 over 2widehat AOB = 90^0) (widehat BOC + widehat COD = widehat BOD) ( Rightarrow widehat COD = widehat BOD – widehat BOC) = (90^0 – 30^0 = 60^0) (widehat COD + widehat DOE = widehat COE) ( Rightarrow widehat DOE = widehat COE – widehat COD) ( = 90^0 – 60^0 = 30^0) c) Các cung có số đo nhỏ hơn 1800 bằng nhau. (overparenBC)= (overparenDE); (overparenAE) = (overparenCD); (overparenAD) = (overparenBD). (overparenAC) = (overparenBE); (overparenAD) = (overparenCE); (overparenCE) = (overparenBD). d) sđ (overparenAE) ( = widehat AOE = 60^0) sđ (overparenBC)( = widehat BOC = 30^0) Ta có số đo của cung (overparenAE) gấp hai số đo của cung (overparenBC). Giaibaitap.me Page 13Câu 10 trang 101 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho tam giác ABC có AB > AC. Trên cạnh AB lấy một điểm D sao cho hạ AD = AC. Vẽ đường tròn tâm O ngoại tiếp tam giác DBC. Từ O lần lượt hạ những đường thẳng vuông góc OH, OK xuống BC và BD ((H in BC,K in BD)). a) Chứng minh rằng OH < OK. b) So sánh hai cung nhỏ BD và BC. Giải 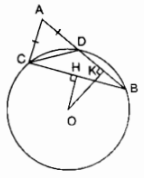 a) Trong ∆ABC ta có: BC > AB – AC (bất đẳng thức tam giác) Mà AC = AD (gt) ( Rightarrow ) BC > AB – AD Hay BC > BD Trong (O) ta có: BC > BD ( Rightarrow ) OH < OK (dây to nhiều hơn gần tâm hơn) b) Ta có dây cung BC > BD Suy ra: (overparenBC) > (overparenBD) (dây to nhiều hơn căng cung to nhiều hơn). Câu 11 trang 101 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Trên dây cung AB của một đường tròn O, lấy hai điểm C và D chia dây này thành ba đoạn thẳng bằng nhau AC = CD = DB. Các nửa đường kính qua C và D cắt cung nhỏ AB lần lượt tại E và F. Chứng minh rằng: a) (overparenAE) = (overparenFB); b) (overparenAE) < (overparenEF). Giải
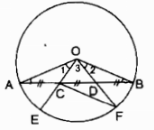 a) ∆OABcân tại O (vì OA = OB nửa đường kính) ( Rightarrow widehat A = widehat B) Xét ∆OAC và ∆OBD: OA = OB (nửa đường kính) (widehat A = widehat B) (chứng tỏ trên) AC = BD (gt) Suy ra: ∆OAC = ∆OBD (c.g.c) ( Rightarrow widehat O_1 = widehat O_2) (1) sđ (overparenAE) ( = widehat O_1) (2) sđ (overparenBF) ( = widehat O_2) (3) Từ (1), (2) và (3) suy ra: (overparenAE) = (overparenBF) b) ∆OAC = ∆BOD (chứng tỏ trên) ( Rightarrow OC = OD) ( Rightarrow Delta OCD) cân tại O nên (widehat ODC < 90^0). Suy ra: (widehat CDF > 90^0) Trong ∆CDF ta có: (widehat CDF > 90^0 Rightarrow CF > CD) nên AC < CF Xét ∆OAC và ∆OCF: OA = OF (nửa đường kính) OC cạnh chung AC < CF Suy ra: (widehat O_1 < widehat O_3) (hai tam giác có 2 cạnh bằng nhau từng đôi một, cạnh thứ 3 không bằng nhau, trái chiều cạnh to nhiều hơn là góc to nhiều hơn). sđ (overparenAE) = (widehat O_1) sđ (overparenEF) ( = widehat O_3) Suy ra: (overparenAE) < (overparenEF). Câu 12 trang 101 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho đường tròn tâm O. Trên nửa đường tròn nửa đường kính AB lấy hai điểm C, D. Từ C kẻ vuông góc với AB, nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F. Chứng minh rằng: a) Hai cung nhỏ CF và DB bằng nhau. b) Hai cung nhỏ BF và DE bằng nhau c) DE = BF. Giải 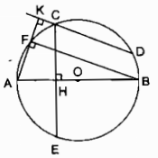 a) ∆ AFB nội tiếp trong (O) có AB là đường kính nên ∆ AFB vuông tại F. ( Rightarrow BF bot AK) (AK bot CD) (gt) Suy ra: BF // CD ( Rightarrow ) (overparenBD) = (overparenCF) (hai cung chắn giữa hai dây tuy nhiên tuy nhiên thì bằng nhau) b) (AB bot CE) tại điểm H nên C và H đối xứng qua trục AB. ( Rightarrow ) (overparenBC) = (overparenBE) (overparenCF) = (overparenBD) (chứng tỏ trên) Suy ra: (overparenBC) + (overparenCF) = (overparenBE) + (overparenBD) Hay (overparenBF) = (overparenDE) c) (overparenBF) = (overparenDE) (chứng tỏ trên) d) BF = DE(hai cung bằng nhau căng hai dây bằng nhau). Câu 13 trang 101 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho đường tròn (O). Gọi I là yếu tố ở chính giữa dây cung AB (Không phải là cung nửa đường tròn) và H là trung điểm của dây AB. Chứng minh rằng đường thẳng IH trải qua tâm O của đường tròn. Giải 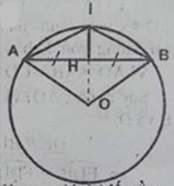 Ta có: (overparenIA) = (overparenIB)(gt) ( Rightarrow IA = IB) (2 cung bằng nhau căng 2 dây bằng nhau) ( Rightarrow I) nằm trên đường trung trực của AB OA = OB (nửa đường kính (O) ( Rightarrow O) nằm trên đường trung trực của AB Suy ra: OI là đường trung trực của AB H là trung điểm của AB, do đó OI trải qua trung điểm H Vậy 3 điểm I, H, O thẳng hàng. Giaibaitap.me Page 14Câu 15 trang 102 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho đường tròn tâm O, nửa đường kính 1,5cm. Hãy vẽ hình vuông vắn ABCD có bốn đỉnh nằm trên đường tròn đó. Nêu cách vẽ. Giải 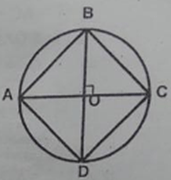 – Vẽ đường tròn (0; 1,5cm) – Vẽ 2 đường kính AC và BD vuông góc với nhau. – Nối AB, BC, CD, DA ta có tứ giác ABCD là hình vuông vắn có 4 đỉnh nằm trên cung tròn (0; 1,5cm). Thật vậy: OA = OC, OB = OD nên tứ giác ABCD là hình bình hành Lại có: AC = BD và (BD bot AC). Vậy: tứ giác ABCD là hình vuông vắn. Câu 16 trang 102 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho đường tròn (O) và hai tuyến phố kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung AC rồi vẽ tiếp tuyến với đường tròn (O) tại M. Tiếp tuyến này cắt đường thẳng CD tại S. Chứng minh rằng (widehat MSD = 2widehat MBA). Giải 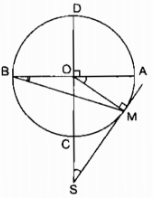 (SM bot OM) (tính chất tiếp tuyến) ( Rightarrow Delta OMS) vuông tại M (widehat MSO + widehat MOS = 90^0) (AB bot CD) (gt) ( Rightarrow widehat MOS + widehat MOA = 90^0) Suy ra: (widehat MSO = widehat MOA) hay (widehat MSD = widehat MOA) (1) (widehat MOA = 2widehat MBA) (góc ở tâm và góc nội tiếp cùng chắn cung (overparenAM)) (2) Từ (1) và (2) suy ra: (widehat MSD = 2widehat MBA) Câu 17 trang 102 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho đường tròn (O) và hai dây AB, AC bằng nhau. Qua A vẽ một cát tuyến cắt dây BC ở D và cắt đường tròn (O) ở E. Chứng minh rằng (AB^2 = AD.AE). Giải
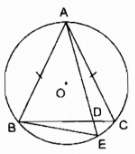 AB = AC (gt) (overparenAB) = (overparenAC) (hai dây bằng nhau căng 2 cung bằng nhau) ( Rightarrow widehat ABC = widehat AEB) (2 góc nội tiếp chắn 2 cung bằng nhau) Xét ∆ABD và ∆ABE: (widehat A) chung (widehat ABC = widehat AEB) (chứng tỏ trên) Hay (widehat ABD = widehat AEB) Suy ra: ∆ABD đồng dạng ∆AEB (AE over AB = AB over AD Rightarrow rm Arm B^2 = AD.AE). Giaibaitap.me Page 15Câu 18 trang 102 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho đường tròn (O) và một điểm M cố định và thắt chặt không nằm trên đường tròn. Qua M vẽ một cát tuyến bất kì cắt đường tròn ở A và B. Chứng minh rằng tích MA.MB không đổi. Giải 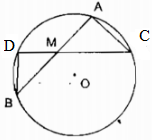 Trường hợp M ở bên trong đường tròn (O) Kẻ cát tuyến AB bất kỳ và kẻ đường thẳng MO cắt đường tròn tại C và D. Xét hai ∆MAC và ∆MBD: (widehat AMC = widehat BMD) (đối đỉnh) (widehat A = widehat D) (hai góc nội tiếp cùng chắn cung (overparenBC) Suy ra: ∆MAC đồng dạng ∆MDB (g.g) ( Rightarrow MB over MC = MD over MA) ( Rightarrow MA.MB = MC.MD) (1) Vì M, O cố định và thắt chặt suy ra điểm C và D cố định và thắt chặt nên độ dài của những đoạn MC và MD không đổi ( Rightarrow ) tích MC.MD không đổi (2) Từ (1) và (2) suy ra tích MA. MB không đổi khi cát tuyến AB thay đổi.
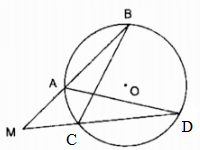 Trường hợp điểm M ở ngoài đường tròn (O) Kẻ cát tuyến MAB bất kỳ của (O) và đường thẳng MO cắt đường tròn (O) tại C và D Xét ∆MAD và ∆MCB: (widehat M) chung (widehat B = widehat D) (hai góc nội tiếp cùng chắn cung (overparenAC)) Suy ra: ∆MAD đồng dạng ∆MCB (g.g) ( Rightarrow MC over MA = MB over MD Rightarrow MA.MB = MC.MD) (3) Vì M và O cố định và thắt chặt suy ra điểm C, D cố định và thắt chặt nên độ dài của những đoạn MC và MD không đổi ( Rightarrow ) tích MC. MD không đổi (4) Từ (3) và (4) suy ra tích MA. MB không đổi khi cát tuyến MAB thay đổi. Câu 19 trang 102 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Để giúp xe lửa chuyển từ một đường ray từ phía này sang một đường ray theo phía khác, người ta làm xen giữa một phần đường ray hình vòng cung (hình 1). Biết chiều rộng của đường ray là AB ( approx 1,1m), đoạn BC ( approx 28,4m). Hãy tính nửa đường kính OA = R của phần đường ray hình vòng cung. Giải 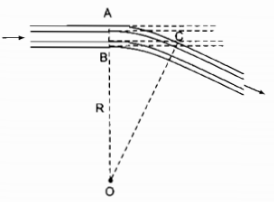 Ta xem hai phần đường ray thẳng là tiếp tuyến của hai phần đường ray vòng cung. Điểm B cố định và thắt chặt nằm trong đường tròn có cung (overparenAC). Đường thẳng OB cắt đường tròn đó tại A và A’. A cố định và thắt chặt và A’ cố định và thắt chặt B là tiếp điểm cung nhỏ trong nên BC là tiếp tuyến của đường tròn (O; OB) ( Rightarrow BC bot OB). Kéo dài BC cắt đường tròn (O; OA) tại C’ ( Rightarrow BC = BC’) (đường kính vuông góc dây cung) Xét ∆BAC và ∆BA’C: (widehat ABC = widehat C’BA’) (đối đỉnh) (widehat ACB = widehat C’A’B) (2 góc nội tiếp cùng chắn cung (overparenAC’)) Suy ra: ∆BAC đồng dạng ∆BC’A’ (g.g) ( Rightarrow BC’ over AB = BA’ over BC) ( Rightarrow BC.BC’ = AB.BA’) mà BC = BC’; BA’ = 2R – AB Suy ra: (BC^2 = ABleft( 2R – AB right)) (left( 28,4 right)^2 approx 1,1.left( 2R – 1,1 right)) ( Rightarrow 2,2R approx 806,56 + 1,21) (R approx 807,77:2,2 = 367,2) (m). Câu 20 trang 102 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho tam giác đều ABC nội tiếp đường tròn (O) và M là một điểm của cung nhỏ BC. Trên MA lấy điểm D sao cho MD = MB. a) Hỏi tam giác MBD là tam giác gì? b) So sánh hai tam giác BDA và BMC. c) Chứng minh rằng MA = MB + MC. Giải 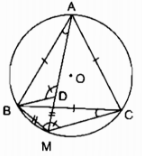 a) MB = MD (gt) ( Rightarrow ) ∆MBD cân tại M (widehat AMB = widehat ACB) (2 góc nội tiếp cùng chắn cung (overparenAB)) Mà (widehat ACB = 60^0) (vì ∆ABC đều) ( Rightarrow widehat AMB = 60^0) hay (widehat DMB = 60^0) Vậy ∆MBD đều b) ∆MBD đều ( Rightarrow widehat DBC + widehat CBM = widehat DBM = 60^0) (1) ∆ABC đều ( Rightarrow widehat ABD + widehat DBC = widehat ABC = 60^0) (2) Từ (1) và (2) suy ra: (widehat CBM = widehat ABD) Xét ∆BDA và ∆BMC: BA = BC (gt) (widehat ABD = widehat CBM) (chứng tỏ trên) BD = BM (vì ∆MBD đều) Suy ra: ∆BDA = ∆BMC (c.g.c) c) ∆BDA = ∆BMC (chứng tỏ trên) ( Rightarrow DA = MC) Ta có: MB = MD (gt) mà AM = AD + DM Suy ra: MA = MD + MC. Giaibaitap.me Page 16Câu 21 trang 102 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho tam giác ABC nội tiếp trong đường tròn tâm O, biết (widehat A = 32^0), (widehat B = 84^0). Lấy những điểm D, E, F thuộc đường tròn tâm O sao cho AD = AB, BE = BC, CF = CA. Hãy tính những góc của tam giác DEF. Giải 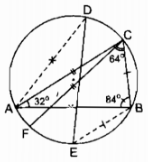
(widehat A = 1 over 2) sđ (overparenBC) (tính chất góc nội tiếp) ( Rightarrow ) sđ (overparenBC) ( = 2widehat A = 2.32^0 = 64^0) BC = BE (gt) ( Rightarrow ) sđ (overparenBC) = sđ (overparenBE) = 640 (widehat B = 1 over 2) sđ (overparenAC) (tính chất góc nội tiếp) ( Rightarrow ) sđ (overparenAC) ( = 2widehat B = 2.84^0 = 168^0) AC = CF (gt) ( Rightarrow ) sđ (overparenCF) = sđ (overparenAC) = 1680 sđ (overparenAC) + sđ (overparenAF) + sđ (overparenCF) = 3600 ( Rightarrow ) sđ (overparenAF) ( = 360^0 – ) sđ (overparenAC) – sđ (overparenCF) = 3600 – 1680. 2 = 240 Trong ∆ABC ta có: (widehat A + widehat B + widehat C = 180^0) ( Rightarrow widehat ACB = 180^0 – left( widehat A + widehat B right)) = (180^0 – left( 32^0 + 84^0 right) = 64^0) sđ (widehat ACB = 1 over 2) sđ (overparenAB) ( Rightarrow ) sđ (overparenAB) ( = 2widehat ACB = 2.64^0 = 128^0) AD = AB (gt) ( Rightarrow ) sđ (overparenAD) = sđ (overparenAB) = 1280 (widehat FED = 1 over 2) sđ (overparenDF) ( = 1 over 2) ( sđ (overparenAD) + sđ (overparenAF)) = (1 over 2.left( 128^0 + 24^0 right) = 76^0) (widehat EDF = 1 over 2) sđ (overparenEF) = (1 over 2) ( sđ (overparenAB) – sđ (overparenAF) – sđ (overparenBE) = (1 over 2.left( 128^0 – 24^0 – 64^0 right) = 20^0) (widehat DFE = 180^0 – left( widehat FED + widehat EDF right)) = (180^0 – left( 76^0 + 20^0 right) = 84^0). Câu 22 trang 102 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Vẽ một tam giác vuông biết cạnh huyền là 4cm và đường cao ứng với cạnh huyền là 1,5cm. Giải 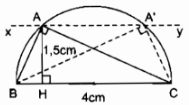 Cách vẽ: – Vẽ đoạn BC = 4cm. – Vẽ nửa đường tròn đường kính BC – Vẽ đường thẳng xy nằm trên nửa mặt phẳng chứa nửa đường tròn và xy // BC, cách BC một khoảng chừng bằng 1,5cm. – Đường thẳng xy cắt nửa đường tròn đường kính BC tại A và A’. Nối AB, AC, A’B, A’C ta có ∆ABC hoặc ∆A’BC cần vẽ. Thật vậy: xy cách BC một khoảng chừng 1,5m < (BC over 2 = 2) cm nên đường thẳng xy cắt nửa đường tròn đường kính BC. Ta lại sở hữu ∆ABC nội tiếp trong nửa đường tròn đường kính BC nên (widehat BAC = 90^0) Có (AH bot BC) và AH = 1,5 cm. Câu 23 trang 103 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho tam giác cân ABC (AB = AC) nội tiếp đường tròn tâm O. Các đường phân giác của hai góc B và C cắt nhau ở E và cắt đường tròn lần lướt ở F và D. Chứng minh rằng tứ giác EBAF là một hình thoi. Giải 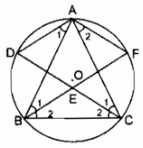
∆ABC cân tại A ( Rightarrow widehat ABC = widehat ACB) (tính chất tam giác cân) BF là tia phân giác của (widehat ABC) (gt) CD là tia phân giác của (widehat ACB) (gt) Suy ra: (widehat B_1 = widehat B_2 = widehat C_1 = widehat C_2) Suy ra: (overparenAD)=(overparenDB)=(overparenAF)=(overparenFC) (widehat A_1 = widehat B_1) (hai góc nội tiếp chắn 2 cung bằng nhau) ( Rightarrow AD//BF) (vì có cặp góc so le trong bằng nhau) Hay AD // EF (1) (widehat A_2 = widehat C_1) (hai góc nội tiếp chắn 2 cung bằng nhau) ( Rightarrow ) AF // CD (vì có cặp góc ở vị trí so le trong bằng nhau) Hay AF // ED (2) (overparenAD) = (overparenAF) (chứng tỏ trên) ( Rightarrow AD = AF) (3) Từ (1), (2) và (3) suy ra: Tứ giác ADEF là hình thoi Giaibaitap.me Page 17Câu 3.1 trang 103 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Mỗi câu tại đây đúng hay sai (A) Góc nội tiếp là góc tạo bởi hai dây của đường tròn đó. (B) Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung. (C) Trong một đường tròn, hai góc nội tiếp không cùng chắn một cung thì không bằng nhau. (D) Trong một đường tròn, số đo của một góc nội tiếp bằng số đo cung bị chắn. (E) Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung. Giải Chọn câu đúng (E) Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung. Câu 3.2 trang 103 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho nửa đường tròn đường kính AB, tâm O. Đường tròn tâm A nửa đường kính AO cắt nửa đường tròn đã cho tại C. Đường tròn tâm B nửa đường kính BO cắt nửa đường tròn đã cho tại D. Đường thẳng qua O và tuy nhiên tuy nhiên với AD cắt nửa đường tròn đã cho tại E. a) (widehat ADC) và (widehat ABC) có bằng nhau không? Vì sao? b) Chứng minh CD tuy nhiên tuy nhiên với AB. c) Chứng minh AD vuông góc với OC d) Tính số đo của (widehat DAO). e) So sánh hai cung BE và CD. Giải 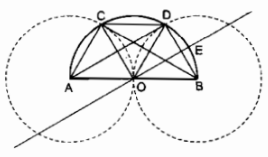 a) Trong đường tròn (O) ta có: (widehat ADC = widehat ABC) (2 góc nội tiếp cùng chắn cung (overparenAC)) b) ∆ACB nội tiếp trong đường tròn (O) có AB là đường kính nên ∆ABC vuông tại C ( Rightarrow CO = OA = 1 over 2AB) (tính chất tam giác vuông) AC = AO (nửa đường kính đường tròn (A)) Suy ra: AC = AO = OC ( Rightarrow ) ∆ACO đều ( Rightarrow widehat AOC = 60^0) ∆ADB nội tiếp trong đường tròn đường kính AB nên ∆ADB vuông tại D ( Rightarrow DO = OB = OA = 1 over 2AB) (tính chất tam giác vuông) BD = BO(nửa đường kính đường tròn (B)) Suy ra: BO = OD = BD ( Rightarrow ) ∆BOD đều ( Rightarrow widehat ODB = widehat BOD = 60^0) (widehat AOC + widehat COD + widehat BOD = 180^0) Suy ra: (widehat COD = 60^0) OC = OD (vì cùng bằng (1 over 2AB)) Suy ra: ∆COD đều ( Rightarrow widehat ODC = 60^0 Rightarrow widehat ODC = widehat BOD) ( Rightarrow ) CD // AB (vì có cặp góc ở vị trí so le trong bằng nhau) c) ∆AOC đều (chứng tỏ trên) ( Rightarrow OA = AC = OC) ∆OCD đều (chứng tỏ trên) ( Rightarrow OC = OD = CD) Suy ra: AC = AO = OD = DC Vậy: tứ giác AODC là hình thoi. d) ∆BOD đều (chứng tỏ trên) ( Rightarrow widehat OBD = 60^0) hay (widehat ABD = 60^0) ∆ADBvuông tại D ( Rightarrow widehat DAB + widehat ABD = 90^0) ( Rightarrow widehat DAB = 90^0 – widehat ABD = 90^0 – 60^0 = 30^0) Vậy (widehat DAO = 30^0) e) OE // AD (gt) ( Rightarrow widehat EOB = widehat DAO = 30^0) (hai góc đồng vị) sđ (overparenBE) ( = widehat EOB = 30^0) sđ (overparenCD) ( = widehat COD) mà (widehat COD = 60^0) (chứng tỏ trên) sđ (overparenCD) = 600 Suy ra: Số đo cung (overparenCD) gấp hai số đo cung (overparenBE). Giaibaitap.me Page 18Câu 24 trang 103 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Hai đường tròn (O) và (O’) cắt nhau tại A và B. Qua A vẽ cát tuyến CAD với hai tuyến phố tròn (C (O), D (O’)). a) Chứng minh rằng khi cát tuyến quay xung quang điểm A thì (widehat CBD) có số đo không đổi. b) Từ C và D vẽ hai tiếp tuyến với đường tròn. Chứng minh rằng hai tiếp tuyến này thích phù hợp với nhau một góc có số đo không đổi khi cát tuyến CAD quay xung quanh điểm A. Giải 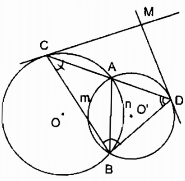 a) Trong ∆ABC ta có: sđ (overparenAnB) sđ (overparenAmB) Vì có A, B cố định và thắt chặt nên sđ (overparenAnB), sđ (overparenAmB) không thay đổi nên (widehat C,widehat D) có số đo không đổi (widehat CBD = 180^0 – left( widehat C + widehat D right)) không đổi Vậy cát tuyến CAD thay đổi số đo (widehat CBD) không đổi. b) Trong (O) ta có (widehat ABC = widehat MCA) (hệ quả góc giữa tia tiếp tuyến và dây) (1) Trong (O’) ta có: (widehat ABD = widehat MDA) (hệ quả góc giữa tia tiếp tuyến và dây) (2) Từ (1) và (2) suy ra: (widehat MCA + widehat MDA = widehat ABC + widehat ABD = widehat CBD) Hay (widehat MCD + widehat MDC = widehat CBD) (không đổi) Trong ∆MCD ta có: (widehat CMD = 180^0 – left( widehat MCD + widehat MDC right)) = (180^0 – widehat CBD) (không đổi) Câu 25 trang 104 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Từ một điểm M cố định và thắt chặt ở bên phía ngoài đường tròn tâm O ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó. a) Chứng minh rằng ta luôn có MT2 = MA.MB và tích này sẽ không phụ thuộc vị trí của cát tuyến MAB. b) Ở hình 2 khi cho MB = 20 cm, MB = 50 cm, tính nửa đường kính đường tròn. Giải 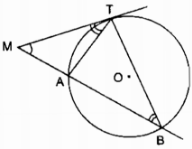 a) Xét ∆MTA và ∆MTB: Có góc (widehat M) chung (widehat MTA = widehat TBA) (hệ quả góc giữa tia tiếp tuyến và dây) Hay (widehat MTA = widehat TBM) Suy ra: ∆MAT đồng dạng ∆MTB (MT over MA = MB over MT) ( Rightarrow MT^2 = MA.MB)  b) Gọi nửa đường kính (O) là R MB = MA + AB = MA + 2R ( Rightarrow MA = MB – 2R) (MT^2 = MA.MB) (chứng tỏ trên) ( Rightarrow MT^2 = left( MB – 2R right)MB) ( Rightarrow R = MB^2 – MT^2 over 2MB) ( = 2500 – 400 over 2.50) = 21 (cm) Câu 26 trang 104 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Ngồi trên một đỉnh núi cao 1km thì trọn vẹn có thể nhìn thấy một vị trí T trên mặt đất với mức cách tối đa là bao nhiêu? Biết rằng nửa đường kính trái đất gần bằng 6400km (h.3)  Giải  Điểm nhìn tối đa là tiếp tuyến Tính từ lúc mắt nhìn đến tiếp điểm của mặt phẳng trái đất (như hình vẽ) Ta có: ∆MAT đồng dạng với ∆MTB ( Rightarrow rm Mrm T^2 = MA.MB) ( Rightarrow MT^2 = MAleft( MA + 2R right)) MA là độ cao của đỉnh núi là 1km, R = 6400 km Thay số ta có: (MT^2 = 1left( 1 + 12800 right) = 12801) MT ( approx 113,1) (km) Câu 27 trang 104 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho tam giác ABC nội tiếp đường tròn (O). Vẽ tia Bx sao cho tia BC nằm trong lòng hai tia Bx; BA và (widehat CBx) = (widehat BAC). Chứng minh rằng Bx là tiếp tuyến của (O). Giải  ∆ABC nội tiếp trong đường tròn (O) có ba kĩ năng xẩy ra của tam giác – ∆ABC là tam giác nhọn – ∆ABC là tam giác vuông – ∆ABC là tam giác tù Xét trường hợp ∆ABC là tam giác nhọn Giả sử Bx không phải là tiếp tuyến của đường tròn (O). Trên cùng nửa mặt phẳng bờ đường thẳng BC chứa tia Bx ta kẻ tia By là tiếp tuyến của đường tròn (O) ( Rightarrow widehat CBy = widehat BAC) (hệ quả của góc giữa tia tiếp tuyến và dây cung) (widehat CBx = widehat BAC) (gt) Suy ra: (widehat CBy = widehat CBx) Ta có By và Bx là hai tia rất khác nhau từ nằm trên cùng một nửa mặt phẳng bờ BC tạo với BC một góc bằng nhau với tính chất đặt tia trên nửa mặt phẳng. Mâu thuẫn với giả sử Bx không phải là tiếp tuyến của đường tròn (O). Vậy Bx là tiếp tuyến của đường tròn (O). Giaibaitap.me Page 19Câu 4.1 trang 104 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho đường tròn tâm O nửa đường kính R. Lấy ba điểm bất kỳ A, B, C trên đường tròn (O). Điểm E bất kỳ thuôc đoạn thẳng AB (và không trùng với A, B). Đường thẳng d trải qua điểm E và vuông góc với đường thẳng OA cắt đoạn thẳng AC tại điểm F. Chứng minh (widehat BCF + widehat BEF = 180^0). Giải  Kẻ tiếp tuyến At của đường tròn (O) At ( bot OA) (tính chất tiếp tuyến) (EF bot OA) (gt) Suy ra: At // EF (widehat EFA = widehat CAt) (so le trong) (widehat CBA = widehat CAt) (hệ quả góc giữa tia tiếp tuyến và dây cung) Suy ra: (widehat EFA = widehat CBA) hay (widehat EFA = widehat CBE) (widehat EFA + widehat EFC = 180^0) (hai góc kề bù) (overparenCBE) + (overparenEFC) = 1800 (1) Trong tứ giác BCFE ta có: (overparenBCF) + (overparenBEF) + (overparenCBE) + (overparenCFE) = 3600 (tổng những góc trong tứ giác) (2) Từ (1) và (2) suy ra: (widehat BCF + widehat BEF = 180^0) Câu 4.2 trang 104 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho tam giác ABC vuông ở A, AH và AM tương ứng là đường cao và đường trung tuyến kẻ từ A của tam giác đó. Qua điểm A kẻ đường thẳng mn vuông góc với AM. Chứng minh: AB và AC tương ứng là tia phân giác của những góc tạo bở AH và hai tia Am, An của đường thẳng mn. Giải  ∆ABCvuông tại A, có AM là đường trung tuyến ứng với cạnh huyền BC ( Rightarrow AM = MB = MC = 1 over 2BC) (tính chất tam giác vuông) ( Rightarrow ) ∆AMB cân tại M ( Rightarrow widehat B = widehat BAM) (1) (mn bot AM) (gt) ( Rightarrow widehat mAM + widehat BAM = 90^0) (2) ∆AHB vuông tại H ( Rightarrow widehat B + widehat BAH = 90^0) (3) Từ (1), (2) và (3) suy ra: (widehat mAB = widehat BAH). Vậy AB là tia phân giác của (widehat mAH). ∆AMC cân tại M ( Rightarrow widehat MAC = widehat C) (4) (mn bot AM) (gt) ( Rightarrow widehat MAC + widehat nAC = 90^0) (5) ∆AHC vuông tại H ( Rightarrow widehat HAC + widehat C = 90^0) (6) Từ (4), (5) và (6) suy ra: (widehat HAC = widehat nAC). Vậy AC là tia phân giác của (widehat HAn) Giaibaitap.me Page 20Câu 28 trang 104 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Các điểm (A_1,A_2,….,A_19,A_20) được sắp xếp theo thứ tự đó trên đường tròn (O) và chia đường tròn thành 20 cung bằng nhau. Chứng minh rằng dây (A_1A_8) vuông góc với dây (A_3A_16). Giải  Đường tròn (O) được phân thành 20 cung bằng nhau nên số đo mỗi cung bằng 3600: 20 = 180. Gọi giao điểm của A1A8 và A3A16 là I. Ta có: sđ (overparenA_1A_3) ( = 2.18^0 = 36^0) (overparenA_8A_16) ( = 8.18^0 = 144^0) Ta có: (widehat A_1IA_3 = 1 over 2) sđ (overparenA_1A_3) + sđ (overparenA_8A_16) (góc có đỉnh ở trong đường tròn (O)) ( Rightarrow ) (widehat A_1IA_3 = 36^circ + 144^circ over 2 = 90^circ ) ( Rightarrow ) A1A8⊥ A3A16 Câu 29 trang 105 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho tam giác ABC vuông góc ở A. Đường tròn đường kính AB cắt BC ở D. Tiếp tuyến ở D cắt AC ở P. Chứng minh PD = PC. Giải  Trong đường tròn (O) ta có (widehat C) là góc có đỉnh ở ngoài đường tròn. (widehat C = 1 over 2) (sđ (overparenAmB) – sđ (overparenAD)) (tính chất góc có đỉnh ở ngoài đường tròn) mà sđ (overparenAmB) = sđ (overparenADB) = 1800 (widehat C = 1 over 2) (sđ (overparenADB) – sđ (overparenAD)) = ( 1 over 2) (sđ (overparenAD) + sđ (overparenDB) – sđ (overparenAD))= ( 1 over 2) sđ (overparenBD) (1) (widehat CDP = widehat BDx) (đối đỉnh) (2) (widehat BDx = 1 over 2) sđ (overparenBD) (góc giữa tia tiếp tuyến và dây cung) (3) Từ (1), (2) và (3) suy ra: (widehat C = widehat CDP Rightarrow Delta PCD) cân tại P. Vậy PD = PC Câu 30 trang 105 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Hai dây cung AB và CD kéo dãn cắt nhau tại điểm E ở ngoài đường tròn (O) (B nằm trong lòng A và E, C nằm trong lòng D và E). Cho biết (widehat CDE) = 75 0, (widehat CED = 22^0), (widehat AOD = 144^0). Chứng minh (widehat AOB = widehat BAC). Giải  Trong đường tròn (O) ta có là góc có đỉnh ở ngoài đường tròn. (widehat E = 1 over 2) (sđ (overparenAD) – sđ (overparenBC)) sđ (overparenAD) = (widehat AOD = 144^circ ) ( Rightarrow ) 22º = (144^circ – sđ overparenBC over 2) Þ sđ (overparenBC)= 144º – 2. 22º = 100º (widehat BAC = 1 over 2) sđ (overparenBC)(tính chất nội tiếp) ( Rightarrow ) (widehat BAC = 1 over 2.100^circ = 50^circ ) Trong ∆ABC ta có (widehat CBE) là góc ngoài tại đỉnh B. ( Rightarrow ) (widehat CBE = widehat BAC + widehat ACB) (tính chất góc ngoài của tam giác) ( Rightarrow ) (widehat ACB = widehat CBE – widehat BAC = 75^circ – 50^circ = 25^circ ) (widehat ACB = 1 over 2widehat AOB) (hệ quả góc nội tiếp) (widehat AOB = 2.widehat ACB = 50^circ ) Vậy (widehat AOB = widehat BAC = 50^circ ) Câu 31 trang 105 Sách Bài Tập. (SBT) Toán 9 Tập. 2 A, B, C là ba điểm thuộc đường tròn (O) sao cho tiếp tuyến tại A cắt tia BC tại D. Tia phân giác của (widehat BAC) cắt đường tròn ở M, tia phân giác của (widehat D) cắt AM ở I. Chứng minh DI ( bot AM). Giải  (widehat BAM = widehat MAC) (vì AM là tia phân giác của (widehat BAC)) ( Rightarrow widehat BM =) (overparenCM) (1) Ta có: (widehat DAM = 1 over 2) sđ (overparenACM) (góc giữa tia tiếp tuyến và dây cung) Hay (widehat DAM = 1 over 2) (sđ (overparenAC) + sđ (overparenCM) ) (2) Gọi N là giao điểm của AM và BC. Ta có: (widehat ANC) là góc có đỉnh ở trong đường tròn (O). ( Rightarrow ) (widehat ANC = 1 over 2) (sđ (overparenAC) + sđ (overparenBM) (3) Từ (1), (2) và (3) suy ra: (widehat DAM = widehat ANC) hay (widehat DAN = widehat AND) Suy ra: ∆DAN cân tại D có DI là tia phân giác nên suy ra DI là đường cao ( Rightarrow ) DI ⊥ AN hay DI ⊥ AM Giaibaitap.me Page 21Câu 32 trang 105 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Trên đường tròn (O; R) vẽ ba dây liên tục bằng nhau AB, BC, CD, mỗi dây có độ dài nhỏ hơn R. Các đường thẳng AB và CD cắt nhau tại I, những tiếp tuyến của đường tròn tại B, D cắt nhau tại K. a) Chứng minh (widehat BIC = widehat BKD) b) Chứng minh BC là tia phân giác của (widehat KBD). Giải  a) (overparenAB) = (overparenBC) = (overparenCD) (gt) (1) Trong đường tròn (O) ta có (widehat BKD) là góc có đỉnh ở ngoài đường tròn. ( Rightarrow widehat BKD = 1 over 2) (sđ (overparenBAD) – sđ (overparenBCD)) = (1 over 2) (sđ (overparenAB) + sđ (overparenAmB) – sđ (overparenBC) – sđ (overparenCD)) (2) Từ (1) và (2) ( Rightarrow widehat BKD = 1 over 2) (sđ (overparenAmB) – sđ (overparenBC)) (3) Trong đường tròn (O) ta có (widehat BIC) là góc có đỉnh ở ngoài đường tròn. ( Rightarrow widehat BIC = 1 over 2) (sđ (overparenAmB) – sđ (overparenBC)) (4) Từ (3) và (4) suy ra: (widehat BIC = widehat BKD) b) (widehat KBC = 1 over 2)sđ (overparenBC) (tính chất giữa tia tiếp tuyến và dây cung) (5) (widehat CBD = 1 over 2) sđ (overparenCD) (tính chất góc nội tiếp) (6) Từ (1), (5) và (6) suy ra: (widehat KBC = widehat CBD). Vậy BC là tia phân giác của (widehat KBD).. Câu 5.1 trang 105 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho đường tròn tâm O nửa đường kính R và dây AB bất kỳ. Gọi M là yếu tố ở chính giữa của cung nhỏ AB. E và F là hai điểm bất kỳ trên dây AB. Gọi C và D tương ứng là giao điểm của ME, MF của đường tròn (O). Chứng minh (widehat EFD + widehat ECD = 180^0). Giải 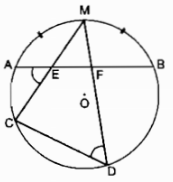 Ta có M là yếu tố ở chính giữa cung nhỏ (overparenAB) ( Rightarrow ) sđ (overparenMA) = sđ (overparenMB) (1) (widehat D = 1 over 2) sđ (overparenMAC) (tính chất góc nội tiếp) ( Rightarrow ) (widehat D = 1 over 2) (sđ (overparenMA) + sđ (overparenAC)) (2) (widehatAEC = 1 over 2) (sđ (overparenMB) + sđ (overparenAC)) (tính chất góc có đỉnh ở trong đường tròn) (3) Từ (1), (2) và (3) suy ra: (widehat D = widehat AEC) (widehat AEC + widehat CEF = 180^circ ) (kề bù) ( Rightarrow )(widehat D + widehat CEF = 180^circ ) (4) Trong tứ giác CEFD ta có: (widehat CEF + widehat D + widehat ECD + widehat EFD = 360^circ ) (tổng những góc trong tứ giác) (5) Từ (4) và (5) suy ra: (widehat ECD + widehat EFD = 180^circ ) Câu 5.2 trang 105 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho đường tròn tâm O nửa đường kính R. Lấy 3 điểm A, B, C trên đường tròn đó sao cho AB = BC = CA. Gọi I là yếu tố bất kỳ của cung nhỏ BC (và I không trùng với B, C). Gọi M là giao điểm của CI và AB. Gọi N là giao điểm của BI và AC. Chứng minh: a) (widehat ANB = widehat BCI) b) (widehat AMC = widehat CBI) Giải  AB = AC = BC (gt) Suy ra những cung nhỏ (overparenAB) = (overparenAC) = (overparenBC) (1) a) (widehat BCI = 1 over 2) sđ (overparenBI) (tính chất góc nội tiếp) hay (widehat BCI = 1 over 2) (sđ (overparenBC)- sđ (overparenCI)) (2) Từ (1) và (2) suy ra: (widehat BCI = 1 over 2) (sđ (overparenAB)- sđ (overparenCI) (3) (widehat ANB = 1 over 2) (sđ (overparenAB)- sđ (overparenCI)) (tính chất góc có ở đỉnh ở ngoài đường tròn) (4) Từ (3) và (4) suy ra: (widehat ANB = widehat BCI) b) (widehat CBI = 1 over 2) sđ (overparenCI)(tính chất góc nội tiếp) Hay (widehat CBI = 1 over 2) (sđ (overparenBC)- sđ (overparenBI)) (5) Từ (1) và (5) suy ra: (widehat CBI = 1 over 2) (sđ (overparenAC)- sđ (overparenBI)) (6) (widehat AMC = 1 over 2) (sđ (overparenAC)- sđ (overparenBI)) (tính chất góc có đỉnh ở bên phía ngoài đường tròn) (7) Từ (6) và (7) suy ra: (widehat AMC = widehat CBI). Giaibaitap.me Page 22Câu 33 trang 105 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho tam giác ABC có cạnh BC cố định và thắt chặt và (widehat A = alpha ) không đổi. Tìm quỹ tích giao điểm của ba đường phân giác trong của tam giác đó. Giải  Chứng minh thuận: Gọi I là giao điểm 3 đường phân giác trong của ∆ABC (widehat IBC = widehat B over 2;widehat ICB = widehat C over 2) ( Rightarrow ) (widehat IBC + widehat ICB = widehat B + widehat C over 2) mà trong ∆ABC ta có: (widehat B + widehat C = 180^circ – widehat A = 180^circ – alpha ) Suy ra: (widehat IBC + widehat ICB = 180^circ – alpha over 2) Trong ∆BIC ta có: (widehat BIC = 180^circ – (widehat IBC + widehat ICB)) Suy ra: (widehat BIC = 180^circ – 180^circ – alpha over 2 = 360^circ – 180^circ + alpha over 2 = 90^circ + alpha over 2) Α không đổi ( Rightarrow widehat BIC = 90^circ + alpha over 2) không đổi. I thay đổi tạo với 2 đầu đoạn BC cố định và thắt chặt một góc bằng 90º + (alpha over 2) không đổi Vậy I nằm trên cung chứa góc 90º + (alpha over 2) vẽ trên BC. Chứng minh hòn đảo: Trên cung chứa góc 90º + (alpha over 2) lấy điểm I’ bất kỳ. Vẽ trên cùng nửa mặt phẳng bờ BC chứa điểm I’ hai tai Bx và Cy sao cho BI’ là phân giác của (widehat CBx,CI’) là phân giác của (widehat BCy). Bx cắt Cy tại A¢. Trong ∆BI¢C ta có: (widehat BI’C = 90 + alpha over 2) ( Rightarrow widehat I’BC + widehat I’CB = 180^circ – widehat BI’C = 180^circ – left( 90^circ + alpha over 2 right) = 180^circ – alpha over 2) (widehat CBA’ = 2widehat I’BC;widehat BCA’ = 2widehat I’CB) ( Rightarrow widehat CBA’ + widehat BCA’ = 2.180^circ – alpha over 2 = 180^circ – alpha ) Trong ∆A¢BC ta có: (widehat BA’C = 180^circ – (widehat CBA’ + widehat BCA’) = 180^circ – (180^circ – alpha ) = alpha ) Vậy quỹ tích giao điểm 3 đường phân giác trong ∆ABC khi (widehat A = alpha ) không đổi, BC cố định và thắt chặt là 2 cung chứa góc (90^circ + alpha over 2) vẽ trên BC.. Câu 34 trang 105 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Dựng cung chứa góc 420 trên đoạn thẳng AB = 3 cm. Giải  Cách dựng: − Dựng đoạn AB = 3 cm − Dựng (widehat BAx = 42^circ ) − Dựng đường thẳng d là trung trực của AB − Dựng tia Ay ⊥ Ax tại A Tia Ay cắt đường trung trực d của AB tại O. − Dựng cung tròn (overparenAmB) tâm O nửa đường kính OA − Dựng điểm O’ đối xứng với O qua AB. − Dựng cung tròn (overparenAm’B) tâm O¢ nửa đường kính O’A. Câu 35 trang 106 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Dựng tam giác ABC, biết BC = 3 cm, (widehat A = 45^0) và trung tuyến AM = 2,5 cm. Giải 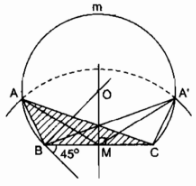 Cách dựng − Dựng đoạn BC = 3cm − Dựng (widehat CBx = 45^circ ) − Dựng trung điểm M của BC − Dựng trung trực BC − Dựng tia vuông góc Bx tại B cắt đường trung trực BC tại O. − Dựng cung tròn (overparenBmC) nửa đường kính OB là cung chứa góc 45º vẽ trên BC. − Dựng cung tròn tâm M nửa đường kính 2,5 cm cắt cung (overparenBmC) tại A và A¢. − Nối AB, AC (hoặc A’B, A’C) ta có ∆ABC (hoặc ∆A’BC) thỏa mãn thị hiếu Đk bài toán. Vì BC = 3 cm, nên nửa đường kính OB = (3sqrt 2 over 2) (cm). Khoảng cách 2 tâm MO = (3sqrt 2 over 2) (cm) (3sqrt 2 over 2 – 2,5 < MO < 3sqrt 2 over 2 + 2,5) nên (O) và (M) luôn cắt nhau. Bài toán luôn dựng được. Giaibaitap.me Page 23Câu 36 trang 106 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho nửa đường tròn đường kính AB cố định và thắt chặt. C là yếu tố trên nửa đường tròn, trên dây AC kéo dãn lấy điểm D sao cho CD = CB. a) Tìm quỹ tích những điểm D khi C chạy trên nửa đường tròn đã cho. b) Trên tia CA lấy điểm E sao cho CE = CB. Tìm quỹ tích những điểm E khi C chạy trên nửa đường tròn đã cho. Giải 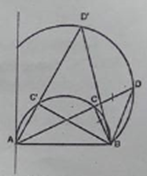
a) Chứng minh thuận: Ta có: (widehat ACB = 90^circ ) (góc nội tiếp chắn nửa đường tròn) Suy ra: (widehat BCD = 90^circ ) CD = CB (gt) Suy ra: ∆BCD vuông cân tại C. ( Rightarrow widehat CDB = 45^circ ) hay (widehat ADB = 45^circ ) AB cố định và thắt chặt. Khi C hoạt động giải trí và sinh hoạt trên nửa đường tròn đường kính AB thì D hoạt động giải trí và sinh hoạt trên cung chứa góc 45º dựng trên đoạn thẳng AB cố định và thắt chặt. Ta có dây AC thay đổi tùy từng vị trí điểm C trên nửa đường tròn đường kính AB. − Dây AC lớn số 1 bằng đường kính của đường tròn. Khi C trùng với B khi đó D trùng với B. Vậy B là yếu tố của quỹ tích. − Dây AC nhỏ nhất có độ dài bằng 0 khi C trùng với A, thì khi đó D trùng ới B’ là giao điểm của tiếp tuyến phố tròn đường kính AB tại A với cung chứa góc 45º vẽ trên AB. Chứng minh hòn đảo: Lấy điểm D’ tùy ý trên cung BB’, nối AD’ cắt đường tròn đường kính AB tại C’. Nối BC’, B’D’. Ta có: (widehat AD’B = 45^circ ) (vì D’ nằm trên cung chứa góc 45º vẽ trên AB). Trong đường tròn đường kính AB ta có: (widehat AC’B = 90^circ ) (góc nội tiếp chắn nửa đường tròn) ( Rightarrow widehat BC’D’ = 90^circ ) Suy ra: ∆BC’D’ vuông cân tại C’ ( Rightarrow ) C’B = C’D’ Vậy quỹ tích những điểm D khi C hoạt động giải trí và sinh hoạt trên nửa đường tròn đường kính AB là cung (overparenBB’) nằm trên cung chứa góc 45º vẽ trên đoạn AB, trong nửa mặt phẳng bờ AB có chứa điểm C. 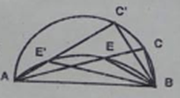 b) Chứng minh thuận: Trong đường tròn đường kính AB ta có: (widehat ACB = 90^circ ) (góc nội tiếp chắn nửa đường tròn) CB = CE (gt) ( Rightarrow ) ∆CBE vuông tại C ( Rightarrow widehat CEB = 45^circ ) (widehat CEB + widehat AEB = 180^circ ) (hai góc kề bù) ( Rightarrow widehat AEB = 135^circ ) AB cố định và thắt chặt, C hoạt động giải trí và sinh hoạt trên đường tròn đường kính AB thì E hoạt động giải trí và sinh hoạt trên cung chứa góc 135º dựng trên đoạn AB cố định và thắt chặt. − Khi dây AC có độ dài lớn số 1 bằng đường kính đường tròn, thì C trùng với B nên E trùng với B ( Rightarrow ) B là một trong những điểm của quỹ tích. − Khi dây AC có độ dài nhỏ nhất bằng 0 thì C trùng với A. Khi đó E trùng A nên A là một trong những điểm của quỹ tích. Vậy E hoạt động giải trí và sinh hoạt trên 1 cung chứa góc 135º vẽ trên đoạn AB nằm trên nửa mặt phẳng bờ AB chứa điểm C. Chứng minh hòn đảo: Lấy E’ bất kỳ trên cung chứa góc 135º. Kẻ AE’ cắt đường tròn đường kính AB tại C’. Nối BE’, BC’. Ta có: (widehat AE’B = 135^circ ) (vì E’ nằm trên cung chứa góc 135º) (widehat AE’B + widehat BE’C = 180^circ ) (kề bù) ( Rightarrow widehat BE’C’ = 180^circ – widehat AE’B = 180^circ – 135^circ = 45^circ ) Trong đường tròn đường kính AB ta có: (widehat AC’B = 90^circ ) (góc nội tiếp chắn nửa đường tròn) Suy ra: ∆E’C’B vuông cân tại C’. ( Rightarrow ) C¢E¢ = C¢B Vậy quỹ tích những điểm E khi C hoạt động giải trí và sinh hoạt trên đường tròn đường kính AB là một cung chứa góc 135º vẽ trên đoạn AB nằm trên nửa mặt phẳng bờ AB chứa điểm C. Câu 37 trang 106 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho nửa đường tròn đường kính AB và C là một điểm trên nửa đường tròn. Trên nửa đường kính OC lấy điểm D sao cho OD bằng khoảng chừng cách CH từ C đến AB. Tìm quỹ tích những điểm D khi C chạy trên nửa đường tròn đã cho. Giải 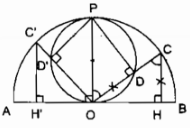
Chứng minh thuận: Từ O kẻ đường thẳng vuông góc với AB cắt nửa đường tròn đường kính AB tại P. O cố định và thắt chặt, đường tròn đường kính AB cố định và thắt chặt suy ra P cố định và thắt chặt. Nối PD. Ta có: OP // CH (vì hai tuyến phố thẳng cùng vuông góc với AB) Xét ∆OCH và ∆OPD: OD = CH (gt) OP = OC (nửa đường kính) (widehat POD = widehat OCH) (so le trong) Suy ra: ∆DOP = ∆HCO (c.g.c) ( Rightarrow )(widehat ODP = widehat CHO) mà (widehat CHO = 90^circ ) nên (widehat ODP = 90^circ ) Khi C hoạt động giải trí và sinh hoạt trên nửa đường tròn đường kính AB thì D thay đổi tạo với 2 đầu đoạn thẳng OP cố định và thắt chặt một góc (widehat OPD = 90^circ ). Vậy D hoạt động giải trí và sinh hoạt trên đường tròn đường kính OP. Chứng minh hòn đảo: Lấy điểm D¢ bất kỳ trên đường tròn đường kính OP. Kẻ OD’ cắt nửa đường tròn đường kính AB tại C’, kẻ C’H’⊥ AB ta phải chứng tỏ OD’ = C’H’. Nối PD’. Xét ∆C’H’O và ∆PD’O (widehat C’H’O = widehat PD’O = 90^circ ) OC’ = OP (nửa đường kính đường tròn tâm O) (widehat D’OP = widehat OC’H’) (so le trong) Suy ra: ∆C’H’O = ∆PD’O (cạnh huyền, góc nhọn) ( Rightarrow ) C’H’ = OD’ Vậy quỹ tích những điểm D khi C hoạt động giải trí và sinh hoạt trên nửa đường tròn đường kính AB là đường tròn đường kính OP. Câu 38 trang 106 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Dựng hình vuông vắn ABCD, biết đỉnh A, điểm M thuộc cạnh BC và điểm N thuộc cạnh CD. Giải 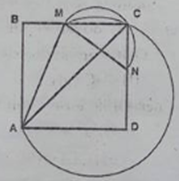 Phân tích: Giả sử hình vuông vắn ABCD dung được thỏa mãn thị hiếu Đk bài toán. Ta cần dựng đỉnh C. Đỉnh C thỏa mãn thị hiếu 2 Đk: − (widehat MCN = 90^circ ) nên C nằm trên cung chứa góc 90º dựng trên MN. − Ta có (widehat ACM = 45^circ ) (vì hình vuông vắn có đường chéo là phân giác) nên C nằm trên cung chứa góc 45º vẽ trên AM. Cách dựng: − Dựng cung chứa góc 90º trên đoạn MN. − Dựng cung chứa góc 45º trên đoạn AM. Hai cung cắt nhau tại C, nối CM, CN. Kẻ AB ⊥ CN tại B, AD ⊥ CN tại D. Ta có tứ giác ABCD là hình vuông vắn cần dựng. Chứng minh: Thật vậy Theo phong cách dựng ta có: (widehat C = 90^circ ,widehat B = 90^circ ,widehat D = 90^circ ) Tứ giác ABCD là hình chữ nhật, có điểm M thuộc BC, điểm N thuộc CD. AC là phân giác của (widehat C.) Vậy: tứ giác ABCD là hình vuông vắn. Giaibaitap.me Page 24Câu 6.1 trang 106 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Dựng một cung chứa góc 600 trên đoạn thẳng AB cho trước. Giải 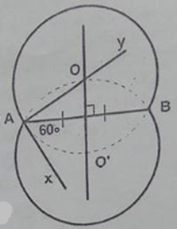
Cách dựng: − Dựng đoạn thẳng AB. − Dựng tia Ax sao cho (widehat BAx = 60^circ ). − Dựng đường thẳng d là trung trực của AB. − Dựng tia Ay ⊥ Ax tại A. − Tia Ay cắt đường thẳng d tại O. − Dựng cung tròn tâm O nửa đường kính OA. − Dựng O’ đối xứng với O qua AB. − Dựng cung tròn tâm O’ nửa đường kính O’A. Ta có cung chứa góc 60º vẽ trên đoạn AB cho trước. Câu 6.2 trang 106 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho đường tròn tâm O nửa đường kính R và điểm A (khác O) ở trong đường tròn đó. Một đường thẳng d thay đổi, luôn trải qua A, cắt đường tròn đã cho tại hai điểm là B và C. Tìm quỹ tích trung điểm I của đoạn thẳng BC. Giải 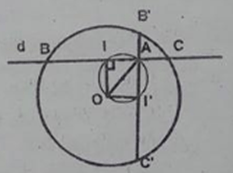 Chứng minh thuận: Đường tròn (O) cho trước, điểm A cố định và thắt chặt nên OA có độ dài không đổi. ∆OBC cân tại O (vì OB = OC nửa đường kính) IB = IC (gt) nên OI là đường trung tuyến vừa là đường cao ( Rightarrow ) OI ⊥ BC ( Rightarrow widehat OIA = 90^circ ) Đường thẳng d thay đổi nên B, C thay đổi thì I thay đổi tạo với 2 đầu đoạn OA cố định và thắt chặt góc (widehat OIA = 90^circ ). Vậy I hoạt động giải trí và sinh hoạt trên đường tròn đường kính OA. Chứng minh hòn đảo: Lấy điểm I’ bất kỳ trên đường tròn đường kính AO. Đường thẳng AI’ cắt đường tròn (O) tại 2 điểm B’ và C’. Ta chứng tỏ: I’B = I’C’. Trong đường tròn đường kính AO ta có (widehat OI’A = 90^circ ) (góc nội tiếp chắn nửa đường tròn) ( Rightarrow ) OI’⊥ B’C’ ( Rightarrow ) I’B’ = I’C’ (đường kính vuông góc với dây cung) Vậy quỹ tích những điểm I là trung điểm của dây BC của đường tròn tâm O khi BC quay xung quanh điểm A cố định và thắt chặt là đường tròn đường kính AO. Câu 6.3 trang 106 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho tam giác ABC có ba góc nhọn. Xác xác lập trí của điểm M trong tam giác sao cho (MA + MB + MC) nhỏ nhất. Giải 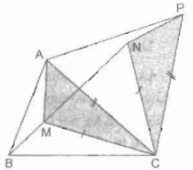 Trong ∆ABC ta lấy điểm M. Nối MA, MB, MC. Ta cần làm xuất hiện tổng MA + MB + MC tiếp sau đó tìm Đk để tổng đó nhỏ nhất. Lấy MC làm cạnh dựng trên nửa mặt phẳng bờ BC chứa điểm A tam giác đều MCN. Suy ra: CM = MN. Lấy AC làm cạnh dựng trên nửa mặt phẳng bờ AC không chứa điểm B tam giác đều APC. Xét ∆AMC và ∆PNC: CM = CN (vì ∆MCN đều) CA = CP (vì ∆APC đều) (widehat MCA + widehat ACN = 60^circ ) (widehat ACN + widehat NCP = 60^circ ) ( Rightarrow widehat MCA = widehat NCP) Suy ra: ∆AMC = ∆PNC (c.g.c) ( Rightarrow ) PN = AM MA + MB + MC = MB + MN + NP Ta có ∆ABC cho trước nên điểm P cố định và thắt chặt nên BM + MN + NP ngắn nhất lúc 4 điểm B, M, N, P thẳng hàng. Vì (widehat CMN = 60^circ ) nên 3 điểm B, M, N thẳng hàng khi và chỉ khi (widehat BMC = 120^circ ) Vì (widehat CNM = 60^circ ) nên 3 điểm M, N, P thẳng hàng khi và chỉ khi (widehat CNP = 120^circ ) Mà ∆AMC = ∆PNC (chứng tỏ trên) ( Rightarrow widehat AMC = widehat PNC = 120^circ ) Vậy MA + MB + MC nhỏ nhất lúc và chỉ khi (widehat BMC = 120^circ ) và (widehat AMC = 120^circ ) Vậy M là giao điểm của 2 cung chứa góc 120º dựng trên BC và AC. Giaibaitap.me Page 25Câu 39 trang 106 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Trên đường tròn tâm O có một cung AB và S là yếu tố ở chính giữa của cung đó. Trên dây AB lấy hai điểm E và H. Các đường thẳng SH và SE cắt đường tròn theo thứ tự tại C và D. Chứng minh EHCD là một tứ giác nội tiếp. Giải 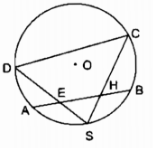 S là yếu tố ở chính giữa của cung (overparenAB). ( Rightarrow ) (overparenSA) = (overparenSB) (1) (widehat DEB = 1 over 2) (sđ (overparenDCB) + sđ (overparenAS)) tính chất góc có đỉnh ở bên trong đường tròn) (2) (widehat DCS = 1 over 2) sđ (overparenDAS) (tính chất góc nội tiếp) hay (widehat DCS = 1 over 2) (sđ (overparenDA) + sđ (overparenSA)) (3) Từ (1) và (2) suy ra: (widehat DEB + widehat DCS = 1 over 2) (sđ (overparenDCB) + sđ (overparenAS) + sđ (overparenDA) + sđ (overparenSA) (4) Từ (1) và (4) suy ra: (widehat DEB + widehat DCS = 1 over 2) (sđ (overparenDCB) + sđ (overparenBS) + sđ (overparenSA) + sđ (overparenDA) ( = 360^circ over 2 = 180^circ ) Hay (widehat DEH + widehat DCH = 180^circ ) Vậy: tứ giác EHCD nội tiếp được trong một đường tròn. Câu 40 trang 106 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho tam giác ABC. Các đường phân giác trong của (widehat B) và (widehat C) cắt nhau tại S, những đường phân giác ngoài của (widehat B) và (widehat C) cắt nhau tại E. Chứng minh BSCE là một tứ giác nội tiếp. Giải 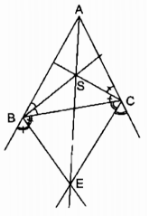 BS ⊥ BE (tính chất hai góc kề bù) ( Rightarrow widehat SBE = 90^circ ) CS ⊥ CE (tính chất hai góc kề bù) ( Rightarrow widehat SCE = 90^circ ) Xét tứ giác BSCE ta có: (widehat SBE + widehat SCE = 180^circ ) Vậy tứ giác BSCE nội tiếp. Câu 41 trang 106 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho tam giác cân ABC có đáy BC và (widehat A = 20^0). Trên nửa mặt phẳng bờ AB không chứa điểm C lấy điểm D sao cho DA = DB và (widehat DAB = 40^0). Gọi E là giao điểm của AB và CD. a) Chứng minh ABCD là tứ giác nội tiếp b) Tính (widehat AED) Giải
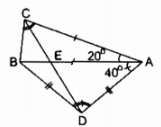 a) ∆ABC cân tại A (gt). ( Rightarrow widehat ACB = widehat ABC) (tính chất tam giác cân) ( Rightarrow widehat ACB = 180^circ – widehat A over 2 = 180^circ – 20^circ over 2 = 80^circ ) ∆DAB cân tại D. ( Rightarrow widehat DBA = widehat DAB) (tính chất tam giác cân) mà (widehat DAB = 40^circ ) (gt) ( Rightarrow widehat DBA = 40^circ ) (widehat ADB = 180^circ – (widehat DAB + widehat DBA) = 180^circ – (40^circ + 40^circ ) = 100^circ ) Trong tứ giác ACBD ta có: (widehat ACB + widehat ADB = 80^circ + 100^circ = 180^circ ) Vậy: Tứ giác ACBD nội tiếp. b) Tứ giác ACBD nội tiếp (widehat BAC = 1 over 2) sđ (overparenBC) (tính chất góc nội tiếp) ( Rightarrow ) sđ (overparenBC)( = 2widehat BAC = 2.20^circ = 40^circ ) (widehat DBA = 1 over 2) sđ (overparenAD) (tính chất góc nội tiếp) ( Rightarrow ) sđ (overparenAD) ( = 2widehat DBA = 2.40^circ = 80^circ ) (widehat AED) là góc có đỉnh ở trong đường tròn ngoại tiếp tứ giác ACBD (widehat AED = 1 over 2)(sđ (overparenBC) + sđ (overparenAD)) ( = 40^circ + 80^circ over 2 = 60^circ ) Giaibaitap.me Page 26Câu 42 trang 107 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho ba đường tròn cùng trải qua một điểm P. Gọi những giao điểm khác P của hai trong ba đường tròn đó là A, B, C. Từ một điểm D (khác điểm P) trên đường tròn (PBC) kẻ những tia DB, DC cắt những đường tròn (PAB) và (PAC) lần lượt tại M, N. Chứng minh ba điểm M, A, N thẳng hàng. Giải 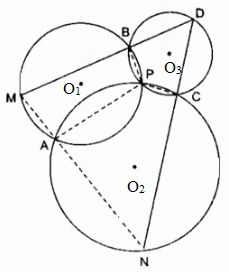 Gọi ba đường tròn tâm O1, O2, O3 (O1) cắt (O2) tại A; (O1) cắt (O3) tại B. (O2) cắt(O3) tại C. Suy ra D là yếu tố nằm trên đường tròn (O3). BD cắt (O1) tại M, DC cắt (O2) tại N. Nối PA, PB, PC; MA, NA. Ta có tứ giác APBM nội tiếp trong đường tròn (O1). (widehat MAP + widehat MBP = 180^circ ) (tính chất tứ giác nội tiếp) (widehat MBP + widehat PBD = 180^circ ) (kề bù) Suy ra: (widehat MAP = widehat PBD) (1) Ta có: Tứ giác APCN nội tiếp trong đường tròn (O2) (widehat NAP + widehat NCP = 180^circ ) (tính chất tứ giác nội tiếp) (widehat NCP + widehat PCD = 180^circ ) (kề bù) Suy ra: (widehat NAP = widehat PCD) (2) Tứ giác BPCD nội tiếp trong đường tròn (O3) ( Rightarrow widehat PBD + widehat PCD = 180^circ ) (tính chất tứ giác nội tiếp) (3) Từ (1), (2) và (3) suy ra: (widehat MAP + widehat NAP = 180^circ ) Vậy ba điểm M, A, N thẳng hàng. Câu 43 trang 107 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho hai đoạn thẳng AC và BD cắt nhau tại E. Biết (AE.EC = BE.ED). Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn. Giải 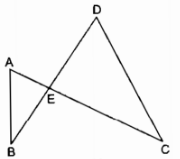 AE. EC =BE. ED (gt) ( Rightarrow AE over ED = BE over EC) Xét ∆AEB và ∆DEC: (AE over ED = BE over EC) (widehat AEB = widehat DEC) (đối đỉnh) Suy ra: ∆AEB đồng dạng ∆DEC (c.g.c) ( Rightarrow widehat BAE = widehat CDE) hay (widehat BAC = widehat CDB) A và D nhìn đoạn BC cố định và thắt chặt dưới một góc bằng nhau nên A và D nằm trên một cung chứa góc vẽ trên BC hay 4 điểm A,B, C, D nằm trên một đường tròn. Câu 7.1 trang 107 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho tam giác ABC có ba góc nhọn. Vẽ những đường cao AI, BK, CL của tam giác ấy. Gọi H là giao điểm của những đường cao vừa vẽ. a) Chỉ ra những tứ giác nội tiếp có đỉnh lấy trong số những điểm A, B, C, H, I, K, L b) Chứng minh (widehat LBH,widehat LIH,widehat KIH) và (widehat KCH) là 4 góc bằng nhau. c) Chứng minh KB là tia phân giác của (widehat LKI). Giải 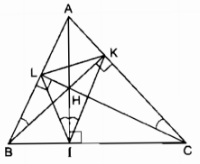
Vì ∆ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC. a) Tứ giác AKHL có (widehat AKH + widehat ALH = 90^circ + 90^circ = 180^circ ) Tứ giác AKHL nội tiếp. Tứ giác BIHL có (widehat BIH + widehat BLH = 90^circ + 90^circ = 180^circ ) Tứ giác BIHL nội tiếp. Tứ giác CIHK có (widehat CIH + widehat CKH = 90^circ + 90^circ = 180^circ ) Tứ giác CIHK nội tiếp. Tứ giác ABIK có (widehat AKB = 90^circ;widehat AIB = 90^circ ) K và I nhìn đoạn AB dưới một góc vuông nên tứ giác ABIK nội tiếp. Tứ giác BCKL có (widehat BKC = 90^circ;widehat BLC = 90^circ ) K và L nhìn đoạn BC dưới một góc vuông nên tứ giác BCKL nội tiếp. Tứ giác ACIL có (widehat AIC = 90^circ;widehat ALC = 90^circ ) I và L nhìn đoạn AC dưới một góc vuông nên tứ giác ACIL nội tiếp. b) Tứ giác BIHL nội tiếp. ( Rightarrow widehat LBH = widehat LIH) (2 góc nội tiếp cùng chắn cung nhỏ (overparenLH)) (1) Tứ giác CIHK nội tiếp. ( Rightarrow widehat HIK = widehat HCK) (2 góc nội tiếp cùng chắn cung nhỏ (overparenHK)) (2) Tứ giác BCKL nội tiếp. ( Rightarrow widehat LBK = widehat LCK) (2 góc nội tiếp cùng chắn cung nhỏ (overparenLK)) hay (widehat LBH = widehat HCK) (3) Từ (1), (2) và (3) suy ra: (widehat LKH = widehat HKI). Vậy KB là tia phân giác của (widehat LKI.) Câu 7.2 trang 107 Sách Bài Tập. (SBT) Toán 9 Tập. 2 Cho đường tròn tâm O nửa đường kính R và hai dây AB, CD bất kì. Gọi M là yếu tố ở chính giữa của cung nhỏ AB. Gọi E và F tương ứng là giao điểm của MC, MD với dây AB. Gọi I và J tương ứng là giao điểm của DE, CF với đường tròn (O). Chứng minh IJ tuy nhiên tuy nhiên với AB. Giải 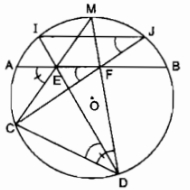 M là yếu tố ở chính giữa của cung nhỏ (overparenAB). (overparenMA) = (overparenMB) (widehat AEC = 1 over 2) (sđ(overparenAC) +sđ (overparenMB)) (góc có đỉnh ở trong đường tròn) (widehat CDM = 1 over 2) sđ(overparenMAC) (tính chất góc nội tiếp) hay (widehat CDF = 1 over 2) sđ(overparenMA) + sđ(overparenAC) Suy ra: (widehat AEC = widehat CDF) (widehat AEC + widehat rmCEF = 180^circ ) (hai góc kề bù) Suy ra: (widehat CDF + widehat rmCEF = 180^circ ) nên tứ giác CDFE nội tiếp ( Rightarrow widehat CDE = widehat CFE) (2 góc nội tiếp cùng chắn cung nhỏ (overparenCE)) hay (widehat CDI = widehat CFE) Trong đường tròn (O) ta có: (widehat CDI = widehat CJI) (2 góc nội tiếp cùng chắn cung nhỏ (overparenCAI)) Suy ra: (widehat CJI = widehat CFE) ( Rightarrow ) IJ // AB (vì có cặp góc ở vị trí đồng tâm bằng nhau) Giaibaitap.me |
Review Bài 52 SBT Toán 9 Tập 2 trang 61 ?
Một số hướng dẫn một cách rõ ràng hơn về Review Bài 52 SBT Toán 9 Tập 2 trang 61 tiên tiến và phát triển nhất .
Chia Sẻ Link Cập nhật Bài 52 SBT Toán 9 Tập 2 trang 61 miễn phí
Người Hùng đang tìm một số trong những Chia Sẻ Link Down Bài 52 SBT Toán 9 Tập 2 trang 61 Free.
#Bài #SBT #Toán #Tập #trang

